안녕하세요 콥스랩(COBS LAB)입니다.
오늘 소개해 드릴 논문은 ‘Effective Diversity in Population Based Reinforce Learning’입니다.
해당 내용은 유튜브 ‘딥러닝 논문 읽기 모임' 중 ‘Effective Diversity in Population Based Reinforce Learning' 영상 스크립트를 편집한 내용으로, 영상으로도 확인하실 수 있습니다. (영상링크:https://youtu.be/AG2uYbbXZuo)
오늘 발표할 내용은 2020년 신경 정보 처리 시스템 학회에서 소개되었던 Effective Diversity in Population Based Reinforce Learning입니다.

Introduction입니다. 먼저 강화 학습의 기초인 Markov Decision Process에 대해서 간단히 알아보겠습니다. 즉 Markov Decision Process는 S A P R 튜플로 구성을 할 수가 있습니다. 여기서 S는 에이전트 상태의 스테이트 집합, A는 취하는 액션의 집합, 그리고 P는 특정 액션을 취하게 될 확률, 그리고 R은 보상에 해당하는 집합이 되겠습니다. 여기서 간단하게 특정 시점에 액션을 취했을 때 여기서 특정 시점 T로부터 그다음 시점인 T+1로까지 전이를 하는 것을 얘기합니다. 마찬가지로 T시점에서 T+1 시점으로 이행했을 때 획득하는 보상을 마찬가지로 리워드라고 정의를 할 수가 있습니다. 그리고 여기서는 포함이 되지 않았는데 에이전트가 네 가지 튜플 값에서 어떤 행동을 취하도록 가이드하는 역할을 policy라고 얘기를 합니다. 이는 상태 값에 집합을 입력을 받아서 액션을 출력하는 함수로 나타낼 수가 있습니다.

그래서 강화 학습에서 여러 종류가 있겠지만 오늘 볼 내용 중에 모델 프리 강화 학습입니다. 이것은 학습과정에서 아까 policy를 업데이트를 할 수 있는 on-policy모델입니다. 업데이트가 불가능한 off-policy 모델로 구분을 할 수가 있습니다. on-policy 모델 경우에는 딥러닝에서 우리가 신경망을 학습할 때 경사 하강법을 즐겨 쓰는 것과 마찬가지로 학습과정에서 policy 변화 양상에 gradient를 관리하는데 집중을 하는 반면에 off-policy에서는 맨 처음에 목푯값에 에이전트가 학습을 잘할 수 있도록 관리를 하는데 초점을 두고 있습니다.
오늘 주로 다룰 내용은 policy를 업데이트할 수 있는 On-policy 강화 학습 모델입니다. 좀 더 구체적으로 얘기를 하면은 On-policy 강화 학습 모델의 목표는 에이전트에 할당된 policy πθ의 변수에 해당하는 θ를 최적화해서 고정된 Marcov decision process의 보상값에 합에 해당하는 R(T)를 극대화하는 내용입니다. 본 모델의 목표 함수는 설명할 보상의 기댓값을 최대화하는데 추정한다고 가정을 할 수가 있습니다. 그리고 policy gradient를 관리를 한다고 했었는데 이 내용은 두 번째 공식으로 정리를 할 수가 있습니다. 첫 번째 공식에서 각 상태에서의 policy 로그 값과 그리고 gradient를 보상한 값에 다시 한번 합친 것이 gradient를 통한 policy 관리 방법입니다.
그리고 본격적으로 evolution strategy에서는 좀 더 나아가는 더 간단한 형식으로 이 목표 함수를 정리를 하게 됩니다. 여기서는 첫 번째 형식으로 가져오되 목표 함수 자체를 블랙박스로 간주해서 자세히 모델링하지는 않고, 대신에 policy를 적용했을 때 보상값과 그리고 d차원에 속하는 τ값과 그리고 여기에 일종의 네 개 변수로서 적용한 람다를 곱한 값을 다 합쳐서 각 에이전트가 취하는 액션에 대한 보상과 그리고 각 차원에 적용했다라든지 다양한 양상 간의 trade off 관계를 표현하기 위해서 좀 더 간단한 형태로 정리를 할 수가 있습니다.

그래서 Marcov decision process 수식으로 알아본 것처럼 쉽게 얘기해서 강화 학습은 특정한 상태에서 어떤 액션을 취해야 최대 보상을 받아낼 수가 있을지를 에이전트를 훈련하는 기법입니다. 그런데 에이전트가 하나만 있을 때는 특정 액션을 취할지 여부를 확률적으로 결정을 하게 됨으로 동일한 세팅으로 반복 학습을 하더라도 학습이 지속되면서 상이한 결과가 나올 수 있습니다. 물론 이런 특이한 사항을 찾는 게 목적이 될 수도 있고 반대가 될 수도 있겠는데 특이한 사항을 찾는 게 아니라면 안정적인 학습 결과를 도출하기 위해서 동일 시간 동안에 다수의 에이전트를 계속 학습을 시켜서 결과를 비교를 할 수 있습니다. 여기서 더 나아가 여러 가지 다수의 에이전트가 학습하여 획득한 각종 결과값을 에이전트 간에 공유를 해서 전체적으로 안정적이면서도 우수한 성능을 도출하려는 방법이 population 또는 군집 기반 훈련에 해당이 됩니다. 이 방법은 인공지능 연구 분야 중에 Neuroevolution 기법에 속하게 되는데 최근 강화 학습 연구에서도 늘어나고 있습니다.

Neuroevolution은 인공지능 연구에 한 분야입니다. 핵심은 솔루션을 계속 반복 계산하면서 확률적으로 우수한 특징을 채택을 하고 불리한 특징을 배제를 하는 과정을 계속 반복한다는 내용입니다. 실제로는 다윈의 진화론에서 영감을 받았다고 하는데 그 원리가 처음에는 같은 조상을 가진 동물이 시간이 지나면서 환경에 적응함에 따라 다양한 양상으로 진화하는 모습을 보고 영감을 받았다고 합니다.
그래서 신경망 같은 경우에는 비지도 학습의 경우 레이블이 필요 없다고 해도 그래도 학습이 원활하게 진행을 하기 위해서는 전체적인 신경만 구조에 대한 정보는 알고 있어야 되는데 Neuroevolution 알고리즘에는 단순히 그냥 주어진 작업에 대한 결과만 알면 됨으로 상대적으로 좀 간단한 신경망에 비해서 간단한 표현입니다.
그리고 결과가 잘 나오면 이쪽으로 계속 후속 학습이 수렴하게 됨으로 어느 정도 성능도 뒷받침이 되고, 그리고 딥러닝처럼 복잡한 구성이 필요한 게 아니기 때문에 크게 컴퓨팅 파워가 많이 소비되지 않습니다.

동일한 에이전트 훈련을 반복을 하거나 아니면 동시에 여러 에이전트를 훈련시켜서 우수한 결과를 공유하는 기법에 대해 설명을 했는데 역으로 특이한 결과값이 나온 훈련을 무시하는 경우가 발생할 수 있습니다.
다양한 상황 속에서 특이한 것을 찾는 게 목적이 될 수도 있고 반대가 될 수 있다고 했는데요. 가령 특이한 상황은 지금까지 내가 알지 못했던 다른 사항을 찾는 것이 목적이라고 해보겠습니다. 위 그림에서 보시면은 한쪽 다리가 없는 개 사진이 있습니다. 이 개는 재활 기간 동안 다리 세 개로 계속 열심히 걸어 다니려고 노력을 했겠죠. 그래서 이 상황을 다시 한번 다족 로봇에 적용을 해봤습니다. 다리 하나를 일부러 부러뜨려서 걸어 다니게 만들어봤습니다. 다리가 멀쩡히 다 있을 때 걸어 다니는 방법으로 계속 학습된 방법을 고수하면, 로봇이 실제로는 다리 하나가 없어지니까 계속 걷는 데 불편함이 있겠죠. 그래서 부러진 다리를 가지고도 다시 멀쩡히 걸어 다니려고 하면은 기존 학습에서 벗어난 특이사항도 마찬가지로 학습을 해야 가능할 것입니다.
여기에 영감을 받은 내용은 오른쪽 그림에 설명이 간단하게 되어 있습니다. 이 내용은 Map elites 알고리즘이라는 내용인데 결과적으로 앞서 설명한 특이상황에서도 학습이 가능하도록 학습에 필요한 공간 정보와 여기에 대응하는 보상을 어떻게 찾아내면 될지를 고찰한 내용입니다. 말 그대로 고차원 공간에 따른 보상값을 어떻게 연결할 수 있는 매핑하는 내용이 됩니다. 이렇게 되면은 내가 원하는 값이 나올 때까지 계속 반복하는 게 아니고 처음부터 학습에 필요한 다양성을 미리 충분히 확보를 해놓은 상태에서 내가 어떤 상황에서도 생각지도 못했던 우수한 학습 결과를 놓치는 일이 없도록 미리 학습에 필요한 차원의 정보를 확보하는 연구를 이른바 Behavioral Characterization 또는 BC라고 통칭을 하고 있습니다.
그래서 이 내용은 딥러닝에서도 gradient descent를 적용했을 때 로컬 미니마 대신에 전체 학습 시 글로벌 미니마 지점이 어디에 있는지 찾아내는 연구와도 일맥상통하는 부분이 되겠습니다.

본 논문의 Contribution입니다. 먼저 BC(Behavioral Characterization)를 좀 더 체계적으로 정의를 한 점, 그리고 policy에 따라서 어떤 액션을 통할 수가 있는지 이른바 Behavior embedding 기법의 가능성을 제시한 것, 그리고 전체 군집에 대한 diversity를 어떻게 하면 알 수 있으니 유사도 매트릭스라는 것을 통해 측정을 하고, 이 내용을 DVD라고 정의를 해서 마지막으로 실제 학습 때 결과를 확인한 점이 되겠습니다.

본격적으로 Diversity via Determinants에 대한 내용을 한번 확인해 보겠습니다. π θ i를 실제 신경망에서는 특정한 vector에 해당하는 것으로 간주합니다.
그러면 이 vector π의 경우에는 각 절댓값과 Marcov decision process에 속한 전체 수의 값으로 나타낼 수가 있습니다. 그래서 위 공식이 embedding이 policy vector와 각 스테이트에 내적이 포함이 되어 있는데, 절댓값이 여기에 포함이 되어 있으므로 실제로 곱셈을 하지 않더라도 어떤 계산하면 동일한 방향으로 결과가 나올 것을 알 수 있습니다.
그래서 (4) 번 공식은 vector i에서의 embedding과 그리고 vector j에서의 embedding이 동일하다면 마찬가지로 두 vector들로 나타내는 policy도 동일하게 표현을 할 수 있다는 것을 의미를 하는 것입니다.
여기서 두 개의 vector값이 같다는 의미는 아니고 결과적으로 두 개의 vector를 정리했을 때 어떤 값을 비교를 하는 것과 실제로 policy를 비교한 값과 같다는 의미를 나타낸 것입니다. 그래서 결과적으로 에이전트가 무슨 테스크를 하던지 상관하지 않고 액션이 속한 차원의 수하고 해당되는 상태의 개수만 알 수 있으면 특정한 에이전트의 Behavior를 조정을 하는 게 가능하다는 의미가 됩니다.

두 가지의 policy를 비교할 수 있는 방법에 대해서 설명드리겠습니다. 예를 들어 d차원에 속하는 x1, x2 두 개의 변수를 갖고 있는 kernel K를 사용합니다. 또한 exp를 사용을 하고 있는데요. 두 개의 policy가 동일한 것을 어떻게 하면 수학적으로 표기하는지 나타냈습니다. x1과 x2의 값이 동일하면은 exp0이 돼서 kernel값이 1이 되겠죠. 이 공식으로는 계산을 할 수는 없는데 어쨌거나 두 개의 policy가 전혀 동일하지 않을 때는 kernel값을 0이라고 가정을 하면 최솟값과 최댓값이 정해지니까 0과 1 사이의 범위에서 policy 간의 유사도를 측정할 수 있는 방법이 생겼습니다.
그리고 군집에 diversity를 정의를 하고 있습니다. m개 policy에 유한한 집합을 θ로 나타내고, 임의의 상태 t에서 kernel 매트릭스에 determinants를 θ에 해당한다고 합니다. 보시면 m개 policy 만큼 두 개의 kernel을 곱하게 되니까 행렬상으로 똑같은 크기의 행렬을 곱하게 되면 우리 determinant 값을 알 수 있습니다.
마지막으로 이 방법에 따른 손실 함수를 정의를 했습니다. DVD 함수는 오른쪽에 있는 함수를 변형을 한 형태입니다.
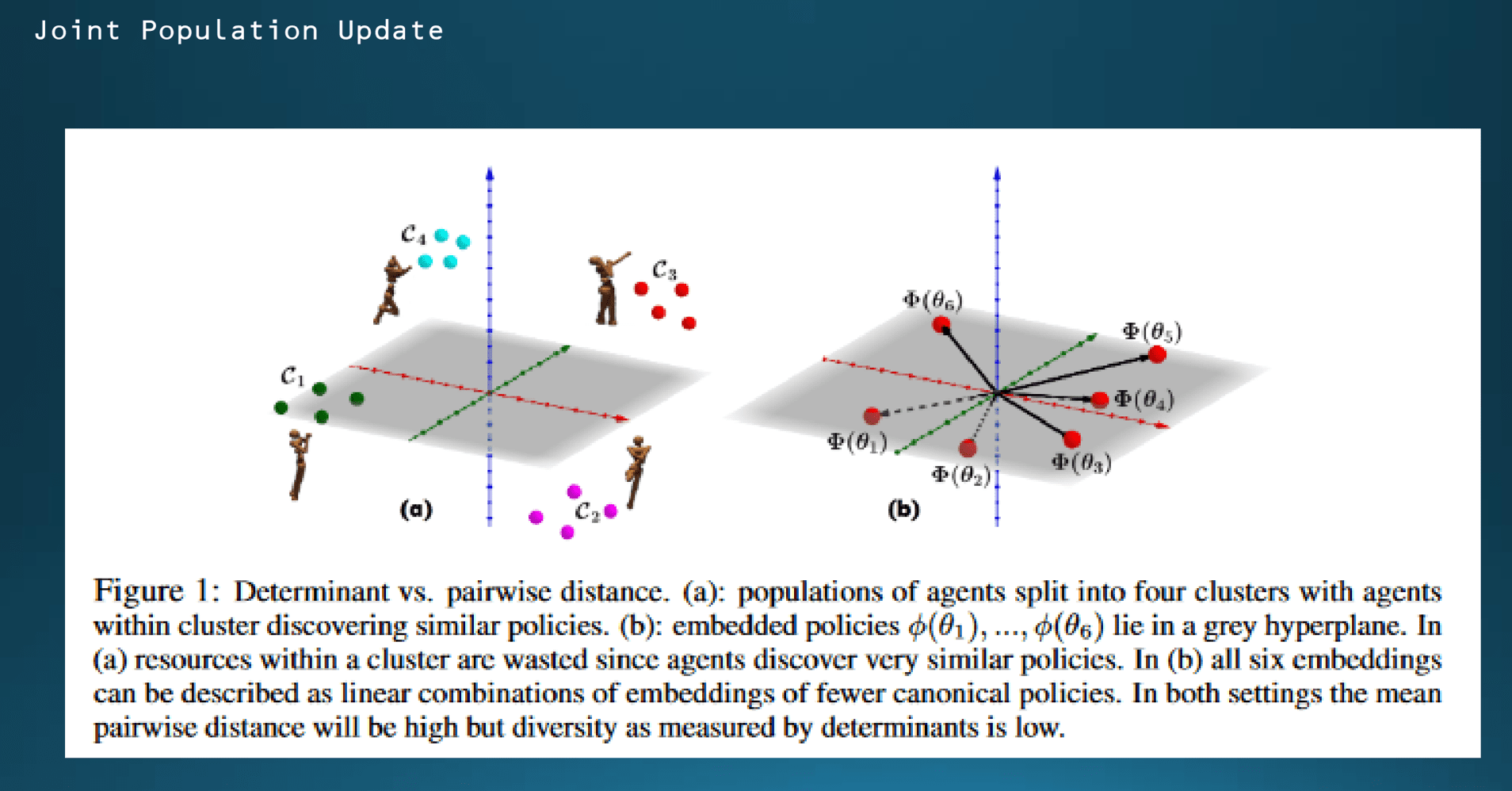
이론적으로 정리한 내용이 어떻게 적용되는지 확인해 보겠습니다. 그림을 보시면 x, y 평면상 인형의 locomotion 결과를 볼 수가 있습니다. 왼쪽은 x, y좌표값에 따른 Pairwise 군집 기반 훈련 결과를 나타낸 것이고 오른쪽에서는 본 논문에서 제시한 DVD 알고리즘 기반 훈련 결과입니다.
왼쪽에서는 학습이 계속 진행되면서 에이전트들이 비슷한 policy를 공유하게 되면서 diversity가 너무 커지는 바람에 결과가 다 분산되는 모습을 확인할 수 있습니다. 반면에 오른쪽 경우에는 변수 θ값을 6가지로 놓고 훈련을 했을 때 서로 다른 policy가 도출되는 것을 알 수 있습니다. 그리고 embedding에 따라서 결과가 수렴하지 않고 명확하게 달라지는 것으로 보아 θ값을 다르게 세팅을 한 걸로 추정됩니다.

다음은 DVD 알고리즘입니다. 그래서 위에서 수식을 설명할 때 M개 policy의 유한한 개수 집합이라고 했었는데 세팅을 어떻게 하느냐에 따라서 무한대에 가까울 수도 있습니다. 그래서 이 논문에서는 M개 policy에서 1부터 M개까지 스테이트만 추출해서 해당 스테이트들로만 policy embedding을 적용한다는 내용입니다.
일단 샘플링을 어떻게 할 것인지는 결국 사용자가 어떻게 튜닝을 할 것인지 설계하느냐에 따라 달라지는 것으로 이해를 하시면 될 것 같습니다. 논문상에서도 샘플링 범위를 어떻게 가져갈 것인지는 향후 개선 가능 영역으로만 정의를 하였습니다.
본 논문에서는 람다 값이 0일 때와 0.5일 때의 경우를 적용하여 실험에 적용합니다.

실험에서 사용될 DVD 기반의 두 가지 알고리즘 구조에 대해서 설명드리겠습니다. 첫 번째로 DVD-ES는 1 policy 모델이고, 각 Timestep마다 policy 집합, θ는 학습에 따른 영향을 받게 됩니다. 다만 보상의 경우는 에이전트별로 따로 계산하는데 diversity는 전체 policy에 대해서 계산을 하게 되고, 다만 계산을 직접 수행하는 것은 아니고 Neuroevolution 알고리즘 설명에서 언급을 한 것처럼 θ에 대한 블랙박스 함수를 처리를 하게 됩니다.
전체적으로 학습에 따라서 On-policy 학습에 따른 성과를 측정하기 위한 gradient 업데이트를 마지막 공식으로 정의를 하고 있습니다. 반대로 DVD-TD3 알고리즘은 Off-policy 모델이고, 그리고 TD3는 2018년에 후지모토 등이 발표하는 이른바 Twin delayed deterministic policy gradient의 줄임말로 Off-policy 강화 학습 모델이 되겠습니다.
여기서는 첫 번째 공식의 군집 diversity term에서 gradient를 계산하는 용도로 본 알고리즘을 제시를 했습니다.
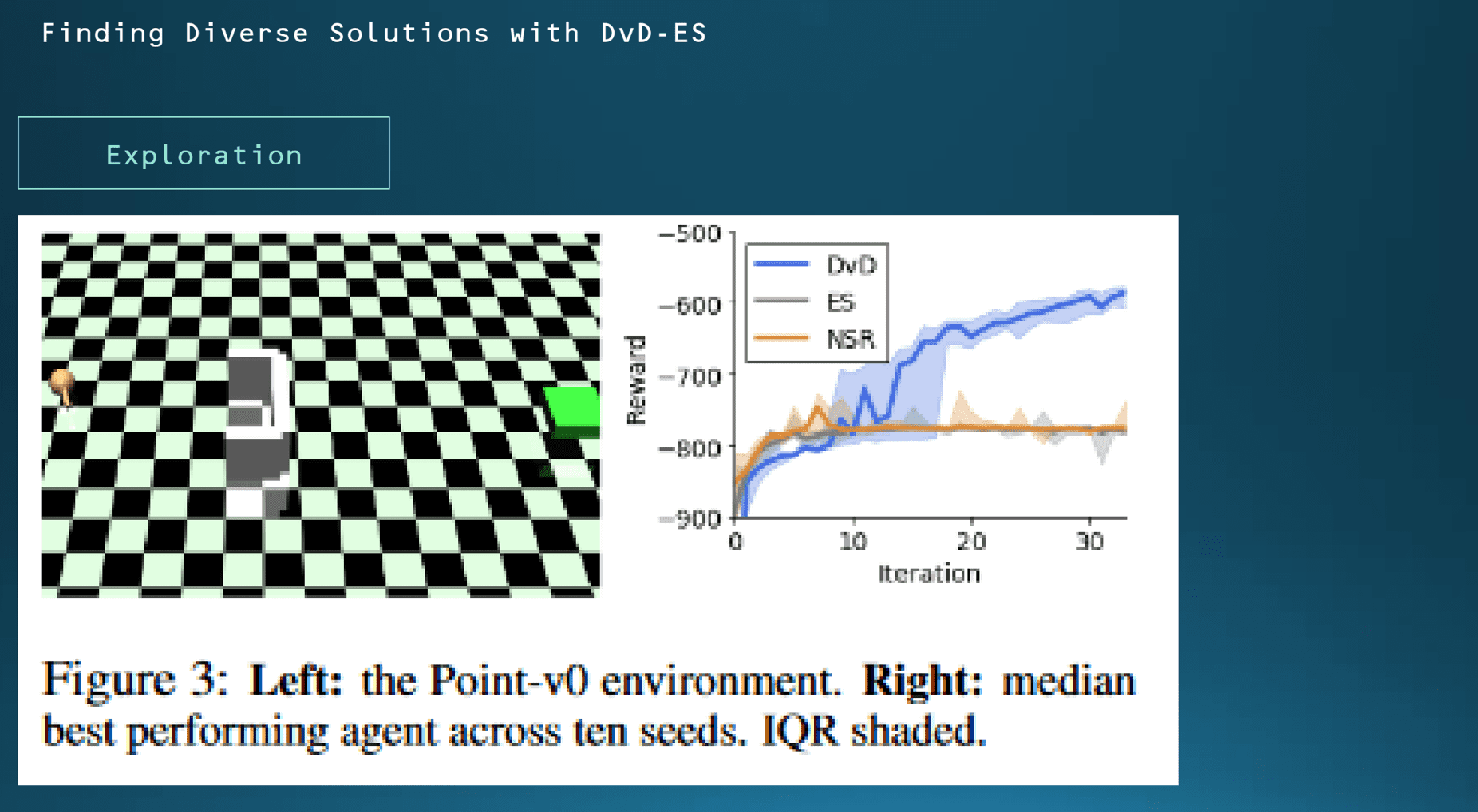
먼저 첫 번째 실험 결과입니다. 먼저 diverse 한 해를 찾아내기 위해서 플레인 한 ES 알고리즘 하고 2018년에 발표된 NSR ES 알고리즘을 비교군으로 제시를 했습니다.
첫 번째로 Exploration 실험의 결과입니다. 이 실험에서는 에이전트가 2차원의 좌표를 갖고 있고 골대에서 멀어질수록 점점 보상값이 마이너스로 커지도록 설정이 되어있습니다. 가령 특정 위치에서 만약에 바로 골대로 가게 되면 반대쪽 골대 벽에 부딪치게 돼서 여기선 리워드를 보상으로 -800점을 보상으로 받게 됩니다. 대신에 골 대벽을 돌아서 갈 경우에는 골을 넣을 때까지는 보상을 받지는 못하지만 일단은 성공하면은 -600점 이상으로 보상을 받게 설정을 했습니다.
군집의 크기를 5로 설정하고 실험을 열 번을 돌렸을 때 오른쪽 그래프에서 보시는 것처럼 나머지 두 개 알고리즘은 계속 점수 그대로 골대 벽에 부딪힌 다음에 더 이상 학습 진척이 없는 반면에 DVD-ES 모델은 성공적으로 골대를 돌아서 계속 골을 넣은 것을 알 수가 있습니다.
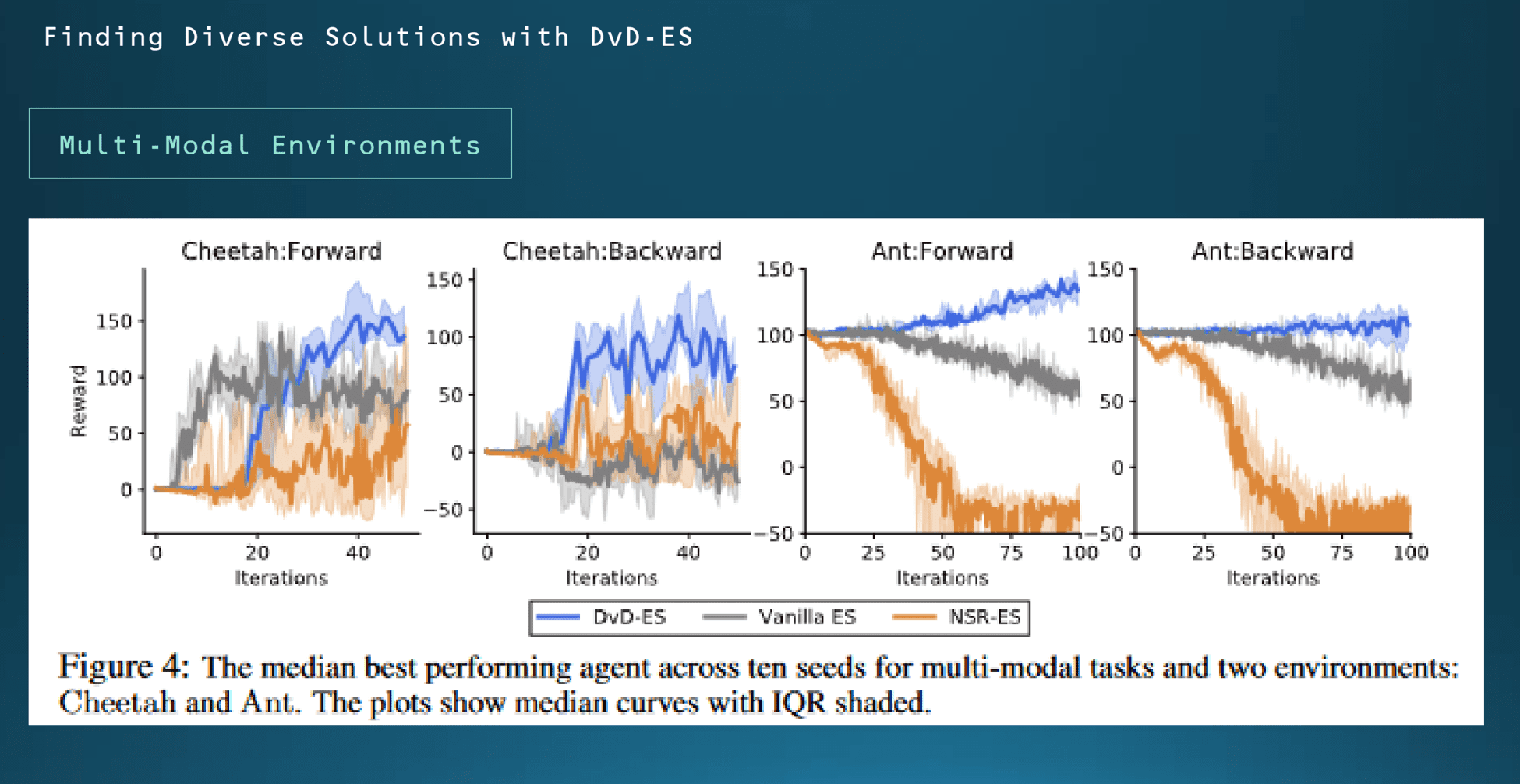
Multi-Modal 환경에서 어떻게 각 모델이 반응하는지를 확인한 것입니다. 여기서는 시뮬레이터에서 치타와 개미의 움직임을 제한한 결과입니다. 군집의 크기는 3으로 설정이 되어있고, 처음에 보시면은 Iteration 20에서 25까지는 다른 비교용 알고리즘보다 치고 나가는 게 보이는데 결과적으로 시간이 지날수록 4가지 케이스 모두 DVD-ES 알고리즘이 가장 학습을 잘한 것을 볼 수가 있습니다.
이 부분은 같은 경우에는 그 치타가 전진할 때, 후진할 때 그리고 개미가 전진할 때, 개미가 후진할 때 각 네 가지 다양한 경우에 대해서 알고리즘이 어떻게 학습을 하는가를 비교했습니다. DVD-ES 알고리즘 자체가 어느 정도에서 diversity에 대해서도 이게 수용 가능성이 높은 만큼 더 우수한 결과가 나온 것을 알 수 있습니다.
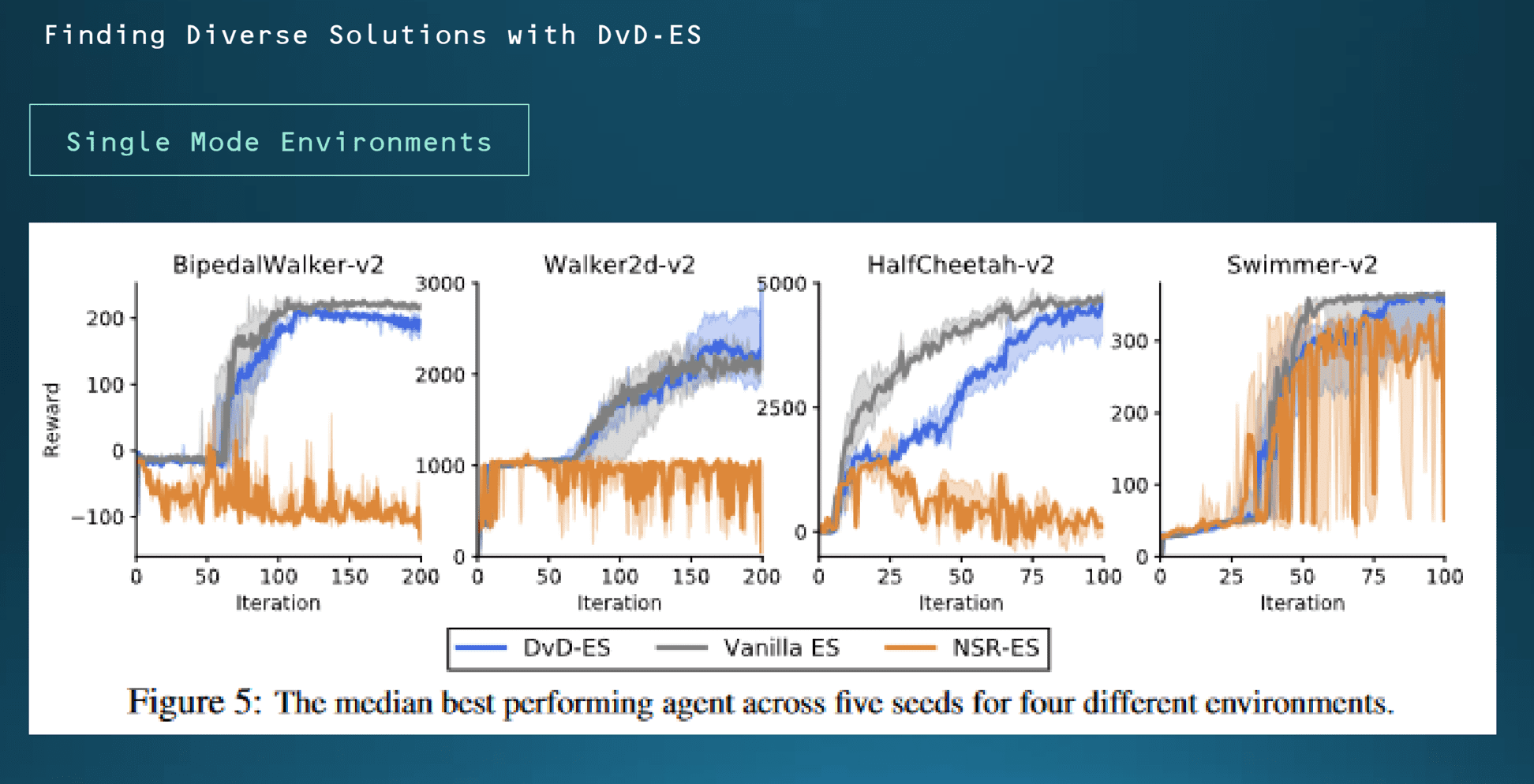
반대로 단일 모드 학습에서 각 알고리즘의 성능을 비교를 했습니다. 재밌게도 diversity가 사실은 많아질수록 실험에서 학습에 불리할 것으로 예상을 했는데 반대로 여기서도 DVD-ES 알고리즘이 선방을 하는 모습을 볼 수 있습니다. 여기서는 앞서 말씀드린 OpenAI 시뮬레이터를 이용하여 계산하였는데 군집의 크기는 5로 설정을 했습니다.
여기서 NSR-ES 알고리즘 같은 경우는 학습이 거의 제대로 되지 않는 모습을 보여주는데, 이 경우에는 보상 함수를 극대화하는 데만 초점이 맞춰져 있어서 실제로 이 세팅이 만약에 적합하지 않은 환경에 알고리즘에 노출될 경우에는 학습 자체가 불가능한 것으로 이해를 할 수 있습니다.

그다음에 Squared Exponential를 선택을 했다고 언급을 했습니다. 여기서 kernel 종류에 따라서 학습 성능에 영향을 받는 게 아닌가 하는 내용을 확인을 한 내용입니다. 결과적으로 kernel이 첫 번째 우리가 사용하는 Squared Exponential 아니면 다른 종류의 kernel이던 종류에 상관없이 유의미하게 학습 결과가 바뀌지는 않는 것을 확인할 수 있습니다.
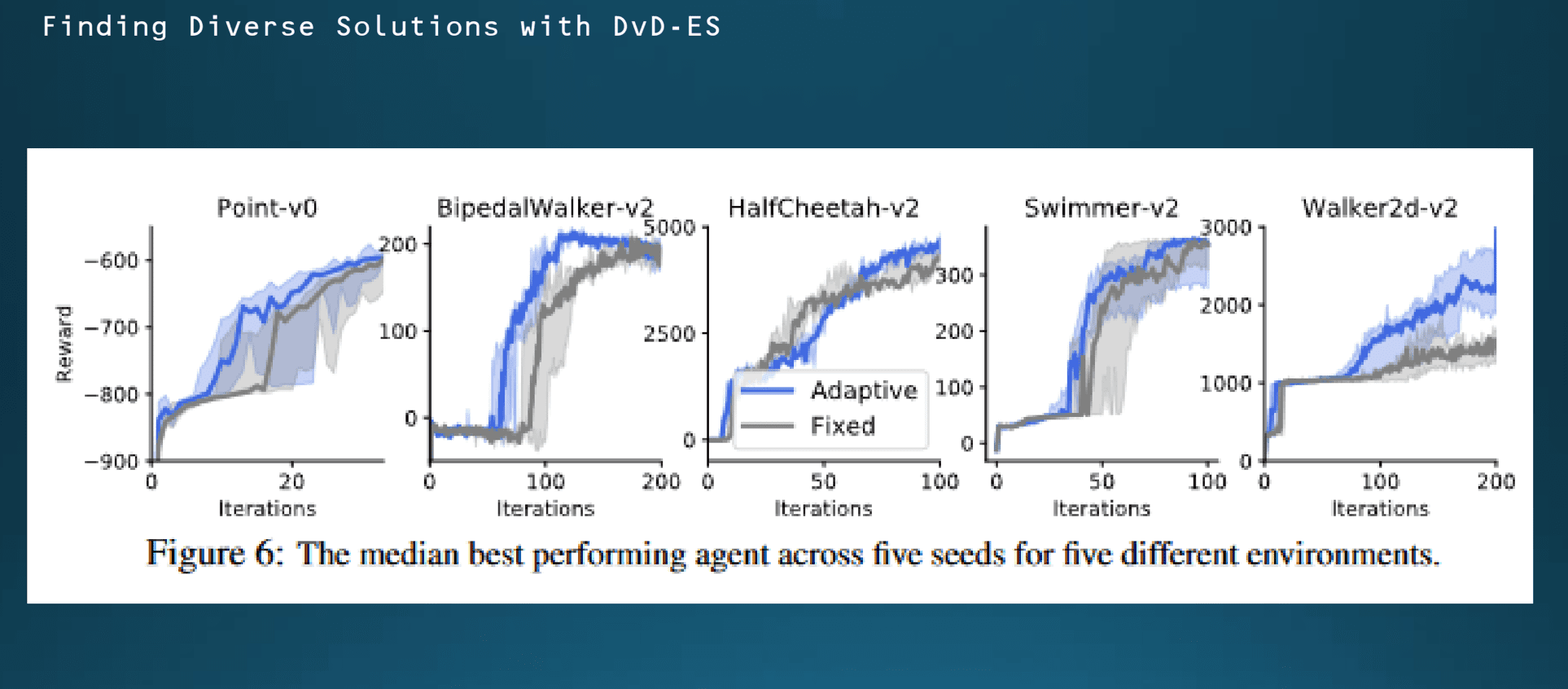
람다 값 조절에 대한 언급이 있었습니다. 회색은 람다 값을 0.5로 고정했을 때 학습결과 그리고 푸른색은 람다 값을 따로 지정하지 않고 학습한 결과입니다. 람다값을 따로 지정을 하지 않고 On-policy 모델이니까 학습진행에 따른 policy를 계속 에이전트가 업데이트를 하게 될건데 어떤 식으로 람다값을 스스로 조절하게 될지에 대한 설명은 논문에서 확인하지 못했습니다.
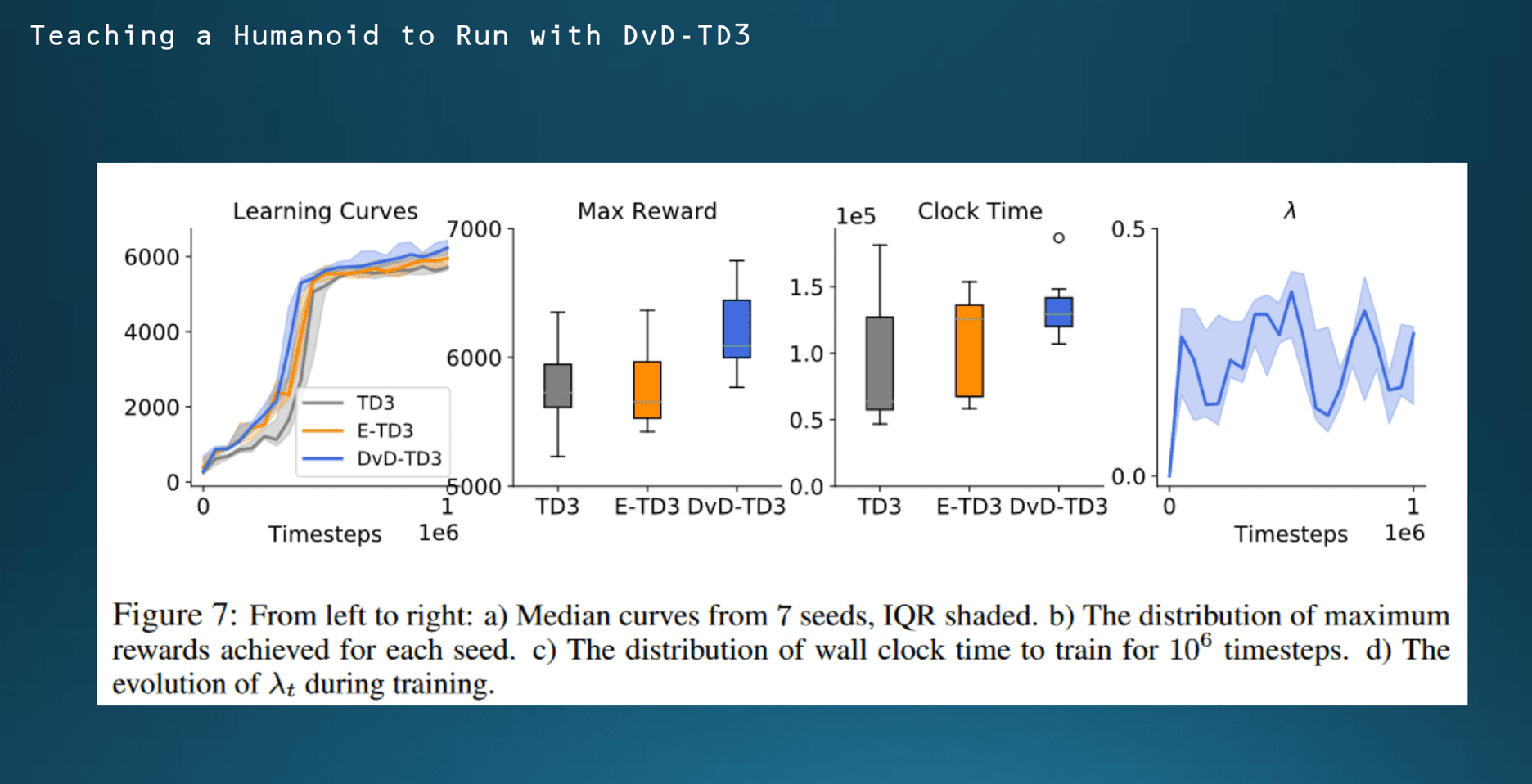
마지막으로 Open AI에서 휴머노이드 환경에서 학습을 진행한 내용입니다. 이른바 휴머노이드 V2 학습이라는 모델이 있는데 여기서 학습에 시간이 굉장히 많이 필요한 것으로 알려져 있는데 최소한 local optimum에 5000점이 배점이 되고 그리고 각 Timestep마다 5점 보너스 점수가 부여가 되니까 에이전트가 굳이 빨리 학습을 최대한 잘할 이유가 없습니다. 그래서 군집 개수를 5개로 놓고 각 에이전트가 개별적으로 policy를 운영하도록 세팅을 했습니다.
여기서는 군집 개수가 1인 경우가 다른 에이전트인 TD3에 해당이 되겠고 군집 개수가 5이고 diversity를 고려하지 않은 경우는 E-TD3라고 정의했습니다. 그리고 DVD-TD3에서는 람다 값은 0으로 설정해서 diversity term을 완전히 삭제를 했습니다. 그리고 모든 방법은 Timestep을 25000번 부여하고 전체 학습을 끝나는 데까지 1,000,000 타입 스텝을 부여했습니다. 실험을 7번 반복해서 결과를 보니까 왼쪽 두 개의 그래프에서는 학습유형 모두 DVD-TD3가 가장 우수한 것으로 나타났습니다.
세 번째는 1,000,000만 Timestep을 소화하는 데 걸리는 시간을 비교를 한 내용입니다. 전체 소요되는 시간도 DVD -TD3가 훨씬 적게 나옵니다.
마지막으로 시간에 따라서 람다 값이 어떻게 바뀌는지에 대한 양상을 그래프로 나타낼 수 있습니다.

결론입니다. 먼저 본 논문에서 주로 사용한 Neuroevolution 기법에서 통하는 모델의 성능을 개선하는 데는 제시하는 Behavioral embedding을 통해서 전향적으로 튜닝이 가능하다는 점, 두 번째로 단일 에이전트를 통한 학습보다 군집 기반 학습을 통해서 더 빠르고 우수한 성능의 학습을 진행하는 게 가능하다는 것, 그리고 다양한 변수가 필요한 환경에서는 diversity term을 더 가져가느냐에 따라서 성능이 더 잘 나올 수가 있다는 점. 이 세 가지로 요약할 수 있습니다.




댓글