안녕하세요 콥스랩(COBS LAB)입니다.
오늘 소개해 드릴 논문은 ‘GCN-LRP explanation exploring latent attention of graph convolutional networks’입니다.
해당 내용은 유튜브 ‘딥러닝 논문 읽기 모임' 중 ‘GCN-LRP’ 영상 스크립트를 편집한 내용으로, 영상으로도 확인하실 수 있습니다. (영상링크:https://youtu.be/u_sy3UfFJsU)
저자가 왜 GCN-LRP 모델을 만들게 되었는지 그 Motivation에 대해 간단히 소개를 하고 관련 연구로 GCN-LRP에 대해 간략히 설명드리겠습니다. 그다음 기존 LRP를 단순히 GCN에 적용하였을 때 생기는 문제점들을 해결하기 위해 본 논문에서 제안하는 방법에 대해 설명을 한 뒤 성능 평가를 하고 결론을 맺겠습니다.

GCN는 node classification과 같은 다양한 Graph 데이터에 성공적으로 적용되고 있습니다. node classification이란 Graph내에 node의 label을 classification 하는 것을 말합니다. 여기서 node의 label은 node의 타입이 될 수도 있고 node의 특성이 될 수도 있습니다. Graph의 node classification이 다른 머신러닝 classification과 다른 점은 Graph 내에 node들이 서로 연결되어 있고 관계를 가지고 있기 때문에 서로 독립적이지 않다는 점입니다.
이러한 node classification은 소셜 네트워크에서 각 사용자의 중요도나 역할을 탐지할 때 사용되며 본 논문에서 사용된 Cora 데이터로 2708개의 논문이 인용되었는지에 따라 서로 연결된 1 large Graph가 있을 때 각각의 논문이 일곱 개의 클래스 중 어느 클래스에 속할지 classify 하게 됩니다. 하지만 Graph가 왜 이런 prediction을 했고, classification을 했는가에 대한 연구는 비교적 최근에 진행되어 아직까지도 내부 논리와 의사 결정 과정에 대해서는 아직 제안된 이해만을 갖고 있습니다.
입력이 deep neural 네트워크에 decision과 어떻게 관련 있는지 설명하기 위해 CAM, EB, Grad-CAM과 같은 다양한 설명방법들이 제안되어왔지만 지금까지 대부분의 XAI 연구는 이미지 처리 딥러닝 모델에서 이루어졌습니다. 따라서 기존 방법들을 단순히 Graph 데이터에 적용한다면 Graph 데이터에 중요한 특징인 데이터 간의 관계를 반영하지 못한다는 문제가 발생하게 됩니다. GCN에 대해서 CAM, EB, Grad-CAM과 같은 방법을 이용하여 설명할 수 있도록 조정되었지만 LRP에 대한 방법은 없어서 본 논문의 저자들은 LRP를 이용하여 GCN를 해석하고자 합니다.

원래 입력값에서 생성된 예측값을 파악하기 위해 LRP가 도입되었으며 이는 입력 데이터가 학습된 모델에서 예측을 서포트하는 방법에 대한 설명 가능성을 제공합니다. 다른 설명방법들과 비교해서 LRP는 neural 네트워크에서 예측을 backward으로 전파하는 것에 대한 더 자세한 설명을 제공하며 LRP의 출력은 입력과 거의 동일한 예측값을 생성하기 위해 신경망에 전달될 수 있습니다.
LRP 모델은 이미지 데이터와 같은 Euclidean 데이터와 Graph 데이터와 같은 non-Euclidean 데이터에 대해 다르게 동작합니다. 이미지 데이터의 경우 LRP의 출력을 사용하여 픽셀 기여를 관 여하 고확 인할 수 있습니다. 이미지는 Euclidean 공간에서 grid 구조화된 데이터이기 때문에 LRP의 설명 출력은 grid값과 학습된 가중치에만 관련이 있습니다.
하지만 Graph 데이터에 경우 Graph 구조가 설명방법에 출력 값에도 영향을 미치기 때문에 GCN을 직접 설명하기 위해 기존 LRP 방법을 그대로 사용할 수 없습니다.

따라서 본 논문에서는 GCN에 대한 새로운 LRP 설명방법을 제안합니다. 또한 이론적으로 latent attention이 어디에서 오고 왜 이런 attention이 데이터의 label 정보 및 모델 훈련으로 거의 바뀔 수 없는지를 분석합니다.
본 논문의 contribution은 크게 세 가지로 볼 수 있습니다. 가장 먼저 GCN에 대한 새로운 LRP기반 설명 방법을 제안합니다. feature 레벨로 로컬 그룹 이나카 테 고리 그룹에서 각 node feature들의 기여로 GCN 모델을 설명할 수 있으며 node 레벨에서 각 node에 기여로 GCN 모델을 설명할 수 있습니다.
다음으로 GCN LRP explanatiion을 통해 실험적으로 GCN의 latent attention을 식별할 수 있습니다. GCN는 인접 node와 비교할 때 classifiy 된 node에 더 많은 attention을 기울이며 모든 인접 node의 동일한 attention을 받지 않는다는 점을 찾아내었습니다. 추가적으로 이론적인 분석을 통해 latent attention은 GCN을 반복적으로 aggregate 하는데에서 나오고 분류된 node와 충분히 공유하는 인접 node를 가진 이웃 node는 다른 node보다 더 많은 attention을 받으며 latent attention은 모델 트레이닝을 통해 거의 변화되지 않는다는 점 또한 보여주었습니다.

GCN이 Graph convolutional network니까 이 모델도 convolution 연산을 수행한다는 것을 알 수 있습니다. convolutional layer의 역할이라고 한다면 그 layer를 거칠 때마다 activation map에 value값을 업데이트시켜준다고 볼 수 있습니다.
GCN의 convolutional layer는 CNN의 convolutional layer와 유사한 점들이 있어서 CNN의 convolutional layer에 대해 간단히 설명드리도록 하겠습니다 convolutional layer가 동작하는 방법은 어떤 이미지 그림에서는 32 x 32 x 32의 RGB 세 개의 채널이니까 depth가 3인 이미지가 있다고 했을 때 그보다 작은 5 x 5 depth는 동일하게 3 필터를 사용하였습니다. 그러면 필터에는 한 층에 25개의 weight가 있고 depth가 3이므로 총 75개 파라미터만 있게 됩니다. 이 필터의 값과 이미지의 75개의 각각의 값을 Dot product 해서 합쳐서 하나의 값을 뽑아내고 이런 필터를 옆으로 이동시키게 되는데 이때 STRIDE를 정해주고 STRIDE만큼 건너뛰면서 값을 쌓아서 새로운 텐서를 만들게 됩니다. 필터 하나마다 두께 1의 activation map이 나오게 되고 필터를 여러 개 씌워서 output 텐서의 depth는 필터를 몇 개 썼느냐에 따라서 정해지는 연산을 convolutional layer의 convolutional 연산이라고 합니다.

GCN을 설명드리기 전에 Graph 데이터의 특징에 대해서도 간략히 설명드리자면 Vertices의 셋과 Edge의 셋으로 이루어져 있는 것을 Graph라고 부릅니다. 1 2 3 4 5 6과 같은 Vertices들이 있고 1과 4 사이에는 Edge가 있고 어떤 두 Vertices 사이에 없는 형태를 Graph라고 정의하게 됩니다.
좌측 Graph를 우측에 표현된 두 개의 matrix를 이용하여 표현할 수 있습니다. node feature matrix는 각 node마다 feature값을 담고 있습니다. 색깔이 동일한 node의 경우 feature가 동일하도록 임의로 설정을 해놓았고 matrix값은 1과 0의 값으로 표현이 될 수도 있고 실수 값으로 표현이 될 수도 있습니다.
가령 본 논문에서 사용한 코라 데이터의 경우에는 n이 node가 되고 feature가 개별적인 단어들이라고 했을 때 해당 논문에 해당 단어가 포함되면 1, 포함되지 않는다면 0의 값으로 나타냅니다.
다음으로 node들 사이가 연결되어 있다면 1, 연결되어 있지 않다면 0으로 표시된 Adjacency matrix가 있으며 node feature matrix와 Adjacency matrix를 이용해서 Graph를 표현할 수 있습니다.

Graph structure 데이터에 대한 러닝을 수행하려면 일반적으로 node feature와 Graph 구조에서 representation를 추출해야 합니다. 이를 위해 Graph 신경망은 neighbor의 feature vector와 representation을 종합해서 각 node에 대한 새로운 representation를 계산합니다. 컴퓨터 비전의 성공적으로 사용된 CNN에서 영감을 받아 연구자들은 aggregation 방법으로 Graph의 convolution operations을 확장하기 시작하였습니다. Graph에서 상태 정보를 결정하는 것은 각 node에 담긴 value, 다시 말해서 node의 feature들입니다.
node feature matrix를 생각해보면 그 안에 담긴 정보가 현재 Graph의 형태는 바꾸지 않으면서 각각의 node 정보만 바꾸게 되기 때문에 그 정보들이 Graph가 나타내는 상태가 무엇이고 또 담고 있는 정보가 무엇인지 알 수 있게 됩니다.
따라서 Graph convolutional layer를 거치면 어떤 node의 정보 즉, node feature matrix안에 있는 value가 업데이트되도록 하면 된다고 할 수 있습니다.
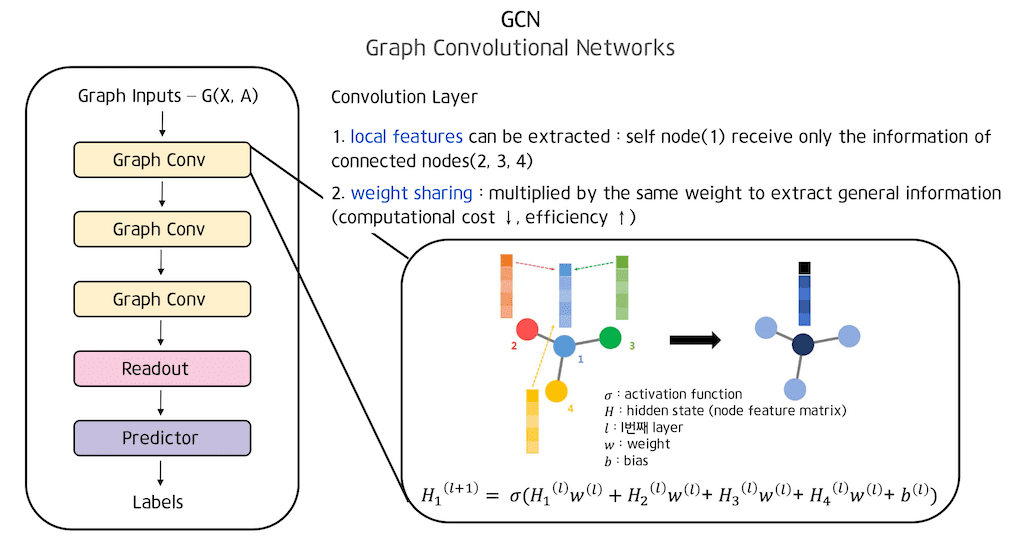
convolution layer의 두 가지 특성은 어떤 로컬 한 근처에 있는 값들만 weight에 들어가서 로컬 한 feature들만 배우고 weight sharing을 한다는 점입니다.
이런 두 가지 특성을 Graph에 어떻게 적용시켜야 할지 생각을 해보면 먼저 리셉트 field는 layer를 하나 거쳐서 각 node의 feature를 계속 업데이트할 때 Edge가 연결되어 있는, 다시 말해서 연결성이 있는 node의 정보만 받아서 업데이트를 수행해주면 됩니다.
다음으로 weight sharing입니다. node의 정보는 feature의 순서가 다 똑같기 때문에 구조가 비슷해서 비슷한 성격을 띠게 됩니다. 따라서 각각의 node feature의 동일한 weight를 곱해줘서 general 한 정보를 뽑아내도록 해줍니다. 이와 같이 weight sharing을 사용해서 곱해 준다면 computational cost도 낮추고 Efficiency 도 높일 수 있는 장점이 생깁니다.
위 수식은 convolutional layer와 동작하는 방식을 적어놓은 수식입니다. w는 weight이며 l은 l번째 layer를 의미합니다. H는 hidden state를 의미하는데 GCN에서는 node feature matrix를 hidden state라고 부릅니다. H1(l+1)은 H1 hidden state의 첫 번째 로우가 l를 통과하고 나왔을 때 그 hidden state 즉 node feature matrix에서 첫번째 node에 해당되는 값을 의미합니다.
앞서 로컬 한 feature, 다시 말해서 근처에 있는 node들만을 이용해서 업데이트시킨다고 말씀드렸는데 H1(l+1) 즉 하나의 layer를 통과하게 되면 H1의 정보는 자기 자신의 정보의 weight를 곱해서 더하고 그 다음에 연결되어 있는 2번, 3번, 4번에 대한 정보들을 받아 weight를 곱한 후 더해준 다음에 activation function을 통과시켜주게 됩니다. 여기서 다음 node에 전달될 때 연결된 node들의 정보만 받고 연결되지 않은 node들의 정보는 들어가지 않기 때문에 convolutional layer처럼 어떤 로컬한 feature를 뽑아낼 수 있게 됩니다.

앞에서 설명드린 식을 Σ를 써서 간단하게 표현하였습니다. node 간의 connectivity를 담고 있는 Adjacency matrix를 활용해서 행렬 연산을 수행해서 더 빠르게 처리할 수 있습니다. node feature matrix H가 있고, weight가 있어서 feature의 개수 x 필터의 개수 사이즈의 weight를 곱해주면 앞서 각 node마다 곱해준 결과를 matrix로 한 번에 구할 수 있습니다.
그래서 Hw (hidden state)의 weight를 곱해준 값에 ij번째가 의미하고 있는 것은 I 번째 node의 J 번째 필터를 씌운 값 즉 새로운 I번째 node들이 로우로 쌓여 있는 형태가 됩니다. 여기서 Adjacency matrix를 곱하면 Adjacency matrix에서 1인 값들은 들어가고 0인 값들은 들어가지 않게 됩니다. 따라서 이 로우에 담겨있는 값들은 해당 node와 연결되어 있는 node들의 feature들을 합한 값이 나와 업데이트 되게 됩니다.
GCN에 대한 전체적인 구조는 좌측 그림과 같으며 Graph 형태의 어떤 인풋이 오고 Adjacency matrix A와 node feature matrix X로 나타내어지는 인풋을 받게 됩니다. 그 인풋의 Graph convolutional layer를 여러 번 수행해주면 더 고차원적인 정보를 담을 수 있게 됩니다.
readout layer에서 마지막 Graph convolutional layer에서 나온 matrix의 LRP를 씌워주어 하나의 vector가 구성되도록 만들어준 다음에 relu와 같은 활성화 함수를 거쳐서 이를 permutation 하게 만들어 줍니다.
마지막으로 predictor layer는 Readout layer에서 나온 Graph feature vector로부터 클래스를 예측하기 위한 linear layer 모듈로 fully connected로 구현하여 결국 모델을 통해 얻고자 하는 하나의 예측값을 얻을 수 있습니다.

XAI 기법은 크게 activation 베이스, backpropagation 베이스, perturbation 베이스 method로 나뉘게 됩니다.
Abm은 이미지 분류에서 입력 데이터에 어떤 부분에 클래스를 예측하는데 영향을 주었는지 시각화하는 방법이며, Bbm은 딥러닝 모델에서 예측 결과를 역추적하여 신경망의 각 계층별 기여도를 측정하는 방법입니다. 마지막으로 Pbm은 입력의 노이즈를 추가하여 모델의 결과를 분석하는 방법이며 그중 본 논문에서 사용된 Layer-wise Relevance Propagation은 대표적인 Bbm기법입니다.
LRP는 neural 네트워크가 어떤 결정을 내렸을 때 어떤 부분을 보고 그런 결정을 내렸는지 분해를 통해 파악하는 방법입니다. 다시 말해서 인풋 x가 d차원으로 주어져있다고 하면 d차원 각각의 feature들이 최종 아웃풋을 도출하는데 서로 다른 영향력을 가지고 있다고 가정하고 이 기여도를 계산하여 분석하게 됩니다.
화면에 그림처럼 수탉 사진을 훈련된 분류기에 넣어주면 그 분류기가 수탉이라는 결과를 내주게 되게 되는데 히트맵에서 각 픽셀들의 relevance 스코어를 색깔로 표시해 두며 해당 예시에는 수탉의 부리나 머리 부분을 보고 해당 입력에 클래스가 수탉임을 출력했다는 것을 알 수 있습니다.

LRP의 동작 과정을 살펴보면 Relevance 스코어를 출력에서 입력 방향 top-down 방식으로 기여도를 재분배하게 됩니다. 여기서 Relevance 스코어라는 것은 x가 출력이 얼마나 많은 영향을 주었는지 x의 변화에 따라 y의 변화가 얼마나 큰 지를 보여줍니다. 이때 각 neuron은 어느 정도의 기여도를 갖고 있으며 각 layer마다 전체 Relevance 스코어는 보존되어야 합니다.

수식과 더불어 조금 더 자세히 설명드리자면 LRP는 neural 네트워크에 activation에 대한 각 인풋 neuron의 contribution을 계산하고, 이런 contribution은 Relevance 스코어로 계층별로 다시 전파합니다.
LRP는 모델 구조와 트레이닝 weight에 의존하기 때문에 LRP 방법은 훈련된 모델이 결정을 내릴 때 모든 관련된 인풋 neuron을 처리하는 방법을 설명합니다. bias가 없는 일반적인 neural 네트워크에서 neuron hjl의 relevance score Rjl은 다음과 같이 정의하게 됩니다.
테일러급수 수식에서 불필요한 텀이 영어로 만들어 적절히 변형해서 나오게 된 수식입니다. 이를 통해 relevance score만으로 분해가 가능해집니다. Σ k는 l+1번째 layer에서 neuron hjl과 관련 있는 모든 neuron들의 합을 의미하며 Σ 0, j는 layer l에서 neuron hjl+1과 관련이 있는 모든 neuron들의 합을 의미합니다.
그리고 앞서 설명드린 것처럼 LRP의 보존 법칙에 따라 neuron이 받은 것과 동일한 amount로 lower layer로 재분배되어야 합니다. 따라서 훈련된 모델의 결정을 위한 인풋 feature의 relevance 스코어를 생성합니다.

본 논문에서는 LRP를 통해 GCN을 설명하기 위해 GCN에서 layer relevance propagation 과정을 Graph convolutional 네트워크를 통한 Forward Reasoning의 역과정으로 처리합니다. Forward Reasoning에서 각 node i는 모든 인접 node의 representation의 가중치 합을 의미하며 각 인접 node j에 대한 가중치는 normarlize Graph, Laplacian l의 i행 j열에 위치한 값과 같습니다. 여기서 Laplacian matrix L은 어떤 node에 degree 정보만 표현하여 대각 행렬은 인접 node의 개수 대각 행렬을 제외하고는 다 0 값을 가지는 degree matrix d에서 Adjacency matrix A를 뺀 행렬로 정의됩니다.

다음으로 각 node는 weight를 곱하여 representation를 변화합니다. 앞서 설명한 Forward Reasoning에 대한 역 프로세스로 먼저 node의 feature vector 구성 요소의 relevance를 할당한 다음 첫 번째 단계에서 계산된 node의 relevance vector를 모든 node에 분해하게 됩니다. 먼저 node feature의 preliminary relevance 스코어를 계산하는 과정은 다음 수식과 같은데 이는 일반적인 LRP 방법과 마찬가지로 node의 feature 필드에서만 relevance 스코어를 전파합니다. 여기서 X~는 self-connections이 추가된 normarlized adjacency matrix에 node feature matrix를 곱한 값이며 W는 trainable weights를 의미합니다.
해당 수식을 통해 node의 feature vector 구성 요소에 초기 relevance 스코어를 할당할 수 있습니다.

다음으로 node의 모든 neighboring node feature에 대한 최종 relevance 스코어를 계산하는 과정은 먼저 L을 통해 모든 인접 node를 찾고 그다음에 Graph의 모든 인접 node에 relevance 스코어를 전파하게 됩니다. 정교화된 Graph Laplacian L과 X~가 위와 같이 정의되었을 때 propagation 식은 RViL과 같이 정의될 수 있습니다.
Σ와 RVjL의 곱과 x kl과 Σ 0, K의 나눗셈은 모두 vector의 엘리먼트 사이에 연산을 나타냅니다. 은닉층의 타당성 계층 간 총합이 일치하게 하는 LRP의 보존 특성 식과 마찬가지로 가중치로 표현하며 ~RVjL를 정의하게 됩니다. 다만 이때 일반적인 LRP에서 weight를 넣는 것과 다르게 인접된 node에 대해서 전파를 하여야 하기 때문에 L를 사용하였습니다.
해당 수식을 통해 어떠한 layer의 relevance 스코어는 전 layer들로 계속해서 propagate 시켜나가 모든 node의 relevance 스코어를 계산할 수 있게 됩니다.

본 논문에서는 많이 알려진 세 개의 Citation 네트워크 데이터 Citeseer, Cora 그리고 Pubmed 데이터를 사용해서 실험을 진행하였습니다.
세 논문 모두 Sparse feature vector는 논문에 단어가 나타나는지 여부를 나타내는 back of words 모델을 사용해서 centitic 리스트에서 생성됩니다. 또한 original Citation 링크가 다이렉트여도 본 논문에서는 Citation 링크를 under edge로 취급하였습니다. 즉, 원래 Graph에는 방향이 있는데 본 논문에서 사용된 예시에는 Graph의 방향이 없는 버전으로 고려합니다. 따라서 A 논문이 B논문을 인용하면 B 논문도 A 논문을 인용한 것으로 간주합니다.
실험에서는 Citation 네트워크 데이터에 대해서 semi - supervised classification GCN 모델을 이용해서 학습을 시킨 다음에 GCN LRP를 이용해서 학습된 GCN 모델을 설명하였습니다.
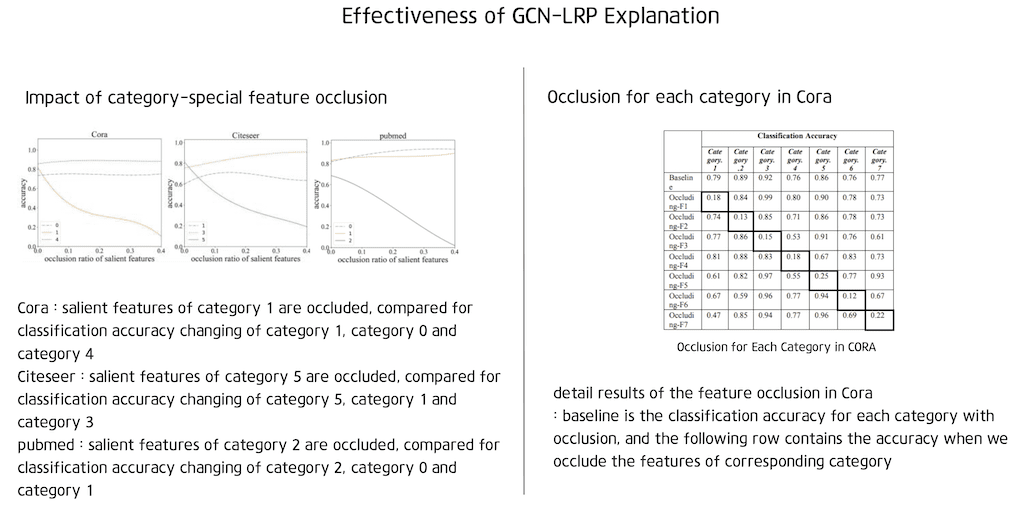
GCN-LRP 설명 기법의 효율성은 설명 방법에 의해 포착된 두드러진 특징을 occluded 함으로써 검증을 진행하였습니다. 다시 말해서 각 카테고리에 대한 node를 분류할 때 분류 정확도의 변화를 알기 위해서 feature들을 occluded 하였습니다. occlusion은 제로 마스크를 사용하여 구현됩니다. 즉 나머지 기능을 일정하게 유지하면서 선택한 feature를 0으로 설정합니다.
category-special feature occlusion의 영향은 좌측 그림과 같은데 feature Occlustion은 해당 범주의 분류 정확도를 떨어뜨리고 Occlusion weight가 40 퍼센트에 도달하면 거의 0에 도달하게 됩니다.
다른 범주에 분류 정확도는 Occlustion에 의해 영향을 받지 않습니다. Cora 데이터에서도 feature Occlusion에 대한 자세한 결과는 우측 표에 나와 있는데 baseline이 occlusion이 있는 각 범주에 대한 분류 정확도이며 다음 행에는 해당 범주의 feature를 occluded 할 때에 정확도입니다.
결과는 GCN-LRP에 의해 탐지된 category special feature의 occlusion이 분류 정확도를 거의 0으로 떨어뜨려서 이러한 feature들을 정확히 찾아낸다는 것을 확인할 수 있습니다.

본 논문에서는 node 레벨 분석에서 node의 모든 feature relevance 스코어의 norm을 node contribution value라고 정의하였습니다. 그리고 node contribution value를 로컬 그룹의 node에서 모든 contribution value의 합으로 나누어서 node contribution ratio로 변환합니다. node 레벨 분석에서는 classify node의 contribution ratio와 neighboring node의 contribution ratio를 비교해보았는데 먼저 classify node의 contribution ratio는 각 로컬 그룹의 모든 node에서 CR의 중앙값 평균 표준편차를 계산하고 모든 node classification task에 대해 분류된 node의 CR을 계산하였습니다. 그다음 모든 분류 작업에 대해 평균 비율을 취합니다.
결과는 좌측과 같으며 분류된 node의 CR은 항상 로컬 그룹의 모든 node의 평균 기여율 보다 크며 3개의 인용 네트워크 데이터셋에서 모든 로컬 그룹에서 가장 큰 node의 CR이 될 확률은 72퍼센트 이상입니다.
다음으로 neighboring node의 contribution ratio에 대한 비교는 전체 contribution interval을 8개의 sub interval로 나누고 ratio of node number(RNN)의 비율은 Ni / N all로 정의하였습니다. 여기서 Ni는 contribution value가 subinterval를 잇는 총 node의 수이고 N all은 모든 neighboring node의 수입니다. 또한 각 subinterval에 대한 node 기여율을 Ci / C all로 정하였습니다. 여기서 Ci는 contribution value가 subinterval에 있는 node의 총 contribution이고 C all은 모든 neighboring node의 총 contribution입니다.
우측 그림에 나와 있듯이 본 논문에서는 모든 classification 테스크에 대해 평균 RNN과 RNC를 취합니다. 결과는 Classify node 외에는 기여율이 큰 node는 몇 개에 불과하고 다른 많은 node는 기여율이 매우 작다는 것을 보여주었습니다.

본 논문에서는 GCN에 대한 새로운 LRP 기반 설명 방법 GCN-LRP를 제안하였습니다. 또한 GCN의 latent attention을 탐구하기 위해 인용 네트워크 데이터셋 및 합성 Graph 데이터셋에 GCN-LRP를 적용하였습니다. 실험을 통해 분류된 node와 몇몇 특별한 neighbor가 다른 node보다 더 많은 attention을 받는다는 것을 발견했습니다.
추가적으로 latent attention은 GCN aggregating을 반복적으로 수행하면서 비롯되고 모델 훈련을 통해 attention은 거의 변경될 수 없다는 것 또한 발견하였습니다.
본 논문의 저자들은 향후 연구로 제시된 연구에서 citation 데이터에 제안되지 않은 다른 데이터셋의 latent attion을 추가로 진행하고자 하며 제안 방법과 결과를 활용해서 Graph 신경망 내부 패턴을 탐색하고 분석하고자 한다고 말하고 있습니다.




댓글