안녕하세요 콥스랩(COBS LAB)입니다.
오늘 소개해 드릴 논문은 ‘Self-Supervised Transformers for Unsupervised Object Discovery using Normalized Cut’입니다.
해당 내용은 유튜브 ‘딥러닝 논문 읽기 모임' 중 ‘Self-Supervised Transformers for Unsupervised Object Discovery using Normalized Cut' 영상 스크립트를 편집한 내용으로, 영상으로도 확인하실 수 있습니다. (영상링크:https://youtu.be/JCEK5nD4MKM)
먼저 Self-Supervised에 대해서 말씀드리겠습니다.

자연어 처리에서의 Self-Supervised learning과 vision Transformer의 차이를 살펴보겠습니다.
자연어 처리에서는 이렇게 my [mask] is cute [sep] king [mask] dogs 이런 식으로 일반적인 문장에서 일정 부분의 단어들을 마스킹하고 그 단어들을 예측하도록 하고 있습니다. 그래서 BERT는 기본적으로 모든 데이터를 학습할 수 있습니다. label이 없더라도 데이터에서 마스크 하면 되기 때문입니다.
반대로 vision Transformer는 label 된 이미지 입력을 작게 쪼개서 입력을 하고 그 다음에 거기에 대해서 label을 맞추는 방식으로 학습을 하게 됩니다. 그래서 label한 데이터만 가능하게 됩니다.
그래서 자연어 처리와 vision Transformer의 Pretrain의 가장 큰 차이는 label된 데이터를 사용하느냐, 사용하지 않느냐 혹은 label된 데이터를 사용한다는 건 데이터의 활용 폭이 적어진다 이렇게 볼 수 있습니다.

이를 해결하기 위해서 Self-Supervised learning들이 시도되고 있습니다. 그중에서 SiT라는 방법을 살펴보겠습니다. SiT는 보시면 이미지가 있는데 이 이미지를 쪼개서 나올 때 노이즈를 가하게 됩니다. Random Drop, Random Replace, Color Distortion, Bluring, Grey-Scale을 통해서 이미지를 왜곡시킨 다음에 마지막에 다시 원본 이미지를 예측하도록 하는 게 이 Image Reconstruction입니다. 이렇게 해서 로스는 원본 이미지와 예측된 이미지에 L1 로스를 가지고 L1 로스가 줄어들도록 학습을 하게 됩니다.

두 번째 방법은 이미지를 Rotation을 시킵니다. 0도 90도 180도 270도 Rotation을 시키고 Rotation에 대한 것이 4가지가 되고 4가지에 대한 확률분포를 구해서 0도인지 90도인지 180도인지 270도인지 맞추는 맞추는 classification 문제로 Rotation Prediction을 하도록 하고 있습니다.

SiT에서 세 번째로 쓰는 방법은 Contrastive learning 각각에 대해서 vector가 비슷한 것과 배치 내에서 다른 것들을 이미지에서 비슷한 vector들을 찾아내도록 하는 Contrastive learning을 통해서 학습을 하게 되면 좋은 특징들을 얻을 수 있는 모델을 학습할 수 있다고 설명하고 있습니다.

다음으로 볼 논문은 DINO라는 아키텍처입니다. 오늘 설명드릴 모델도 DINO를 기반으로 해서 만들어진 모델입니다. 원본 이미지가 있으면 augmentation를 각각 다른 방법으로 합니다. Augmentation을 하고 그다음에 이미지를 얻습니다. 여기서 보시면 이쪽에 Teacher, Student 이렇게 이미지를 만들고 각각 이미지를 집어넣습니다. 다음 나온 곳에서 소프트맥스를 각각 하게 되는데 Teacher는 Teacher 예측값에서 센터를 뺀 값, Student는 예측값 그대로 해서 나올 두 개의 확률에 대해서 크로스엔트로피를 구하고 엔트로피 로스를 줄여주는 식으로 학습을 하게 됩니다. 그리고 Student만 backpropagation을 하고 그 다음에 EMA(Exponential Moving Average)를 통해서 Student에 있는 웨이트를 피쳐로 옮겨가는 방식으로 Teacher를 학습하지 않고 Student에 있는 웨이트로 옮겨가는 방식으로 학습을 합니다.

Psuedo code입니다. 원본 이미지가 있을 때 Augment를 각각 다른 방법을 해서 x1과 x 2가 있으면 Student에도 x1과 x2를 넣고 그다음에 Teacher에도 x1과 x2를 넣고 나온 친구들을 로스 함수를 통해서 t1과 s2 그리고 t2와 s1 이렇게 다르게 해서 로스를 구하고 이 로스를 minimize 하게 됩니다. 그리고 gradient를 구하고 Teacher의 파라미터에다가 l 값에다가 1-l에서 Student 파라미터를 해줍니다. 이때 람다 값 l은 0.996에서 1 사이기 때문에 매우 작은 값입니다. 그래서 Student가 매우 작게 반영돼서 지속적으로 Teacher가 반영된다 보시면 됩니다.
그다음에 센터값은 중앙값을 의미하는데 Teacher에 있는 값의 중앙값인데 이전 센터값과 새로운 센터 값을 averaging 해가면서 센터값을 계산하게 되고 이렇게 하면 모델이 어떤 학습이 안 되는 것들을 막을 수 있다고 합니다.
h함수를 보게 되면 Teacher는 약간 backpropagation하지 않기 때문에 detach를 하고 그다음에 Student는 바로 템퍼러쳐라고 해서 소프트맥스 취했는데 Teacher는 센터값을 빼준 상태에서 temperature를 나눠서 했습니다. 그리고 나서 negative로 log likelihood를 구한 것을 알 수 있습니다.

이렇게 했더니 신기하게도 이 오브젝트에서 보시면 attention Map이 이렇게 잘 잡아내고 있습니다. 또 칫솔도 attention Map을 잘 잡아내고 있습니다.

이런 사진에서도 주요한 이미지들을 잘 뽑아내고 있는 것을 볼 수 있습니다. 이렇게 DINO 방법으로 학습을 하게 되면 중요한 이미지들이 좋은 vector를 갖게 됩니다.
Supervised 방식과 DINO를 비교했을 때도 DINO가 훨씬 더 좋은 attention Map을 가지고 있는 것을 알고 있습니다. 그중에 비슷한 vector들이 같은 곳을 잘 향하고 있다 이렇게 볼 수 있을 것 같습니다.

그다음에 LOST 함수입니다. LOST 모델인데 DINO backbone을 그대로 사용하고 있고 DINO backbone에서 attention Map보다 좀 더 좋은 방법으로 어떤 객체를 뽑아내는 그런 방법을 제시했습니다. 예를 들어 배 이미지가 있을 때 이미지를 넣어서 쪼개는데 좀 크게 쪼개보겠습니다. 우리가 봤을 때 1 2 3은 아마 비슷한 vector를 갖게 될 것 같고 이미지가 비슷하니까 또 5 6 번도 비슷할 것 같습니다. 그리고 4 7 8 9가 비슷할 것 같고 6번과 4번 은 비슷하지 않을까 이렇게 가정을 해보고 통과하게 되고 이때 두 vector들간의 1번과 2번,1번과 3번 이렇게 두 vector에 dot product를 하고 그 다음에 그 친구가 0보다 크면 90도 이내라는 얘기입니다. 90도 이내에 있으면 1이고 그렇지 않으면 0이라고 했습니다.
이것들을 쭉 그려보면 Adjacency Matrix가 있습니다. 1번의 경우에는 2 3번과 비슷하고 2번의 경우 1 3번과 비슷하고 3번의 경우에는 2번과 비슷하고 4번의 경우에는 6 7 8 9번 이런 식으로 매트릭스를 구할 수 있을 것 같습니다. 그리고 다 썸 하면 첫 번째 몇 개가 있는지 연결되는지 볼 수 있습니다.
아래쪽에 보시면 Degree Matrix를 구할 수 있습니다. 1번은 2개 하고 연결되어 있고 2번은 두 개 이런 식으로 구할 수가 있게 되고 이 값 중에서 가장 작은 값 seed라고 얘기하고 있으면서 Degree matrix를 만들고 이 중에 가장 작은 것을 Seed로 잡습니다.
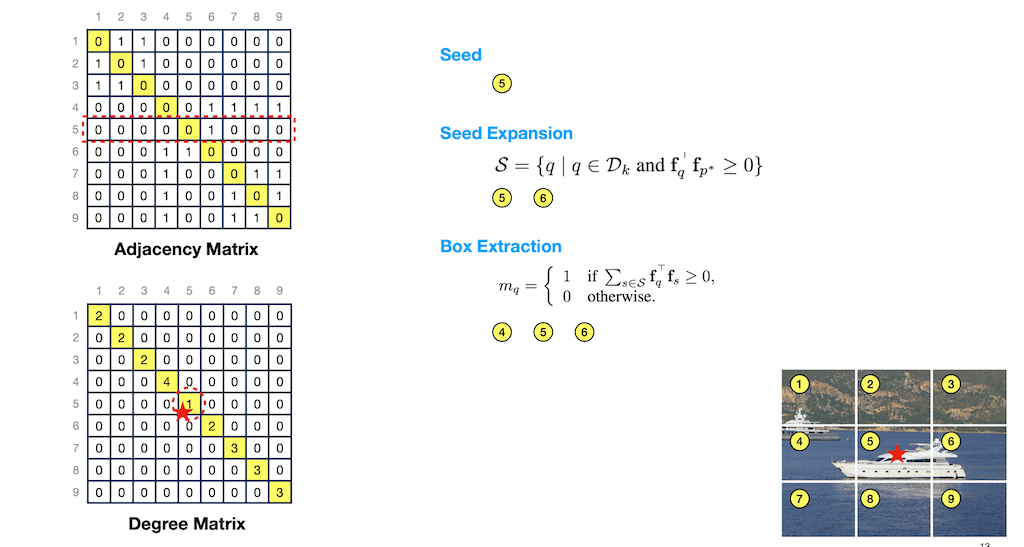
전체를 쭉 보면 6번까지 들어가 있습니다. 그래서 6번까지를 이런 식으로 여기 0보다 큰 것들을 잡으면 5번과 6번이 Seed가 되고 이걸 가지고 Box Extraction를 하게 되면 5 6번에 있는 모든 1인값들이 4 5 6번 이렇게 있으니까 4 5 6 번 이렇게 해서 거기다가 bounding box를 치겠다는 게 LOST가 제시하는 모델입니다.

LOST가 이렇게 했더니 위 같은 이미지가 있을 때 히든 값들이 잡히고 오브젝트가 잘 잡히고 표현되는 것을 알 수가 있습니다. 그래서 DINO 보다 LOST를 썼더니 더 좋아졌다. 이렇게 설명하고 있습니다.

다음은 Token Cut입니다.
LOST 하고 비슷하니까 동일하게 이렇게 이미지를 9 개를 쪼개서 넣으면 similarity 함수가 달라졌습니다. 여기 보시면 이런 식으로 Cosine 세타 값을 구합니다. 그래서 Cosine 세타가 하이퍼 파라미터를 줬는데 0.2보다 클 때는 1이고 나머지는 le-5승 이런 작은 값을 줬습니다.
fully connected 그래프 만들겠다고 얘기를 하고 있는데 0이라고 가정을 해도 크게 문제가 없을 것 같습니다. 이렇게 했을 때 이런 그래프를 그릴 수 있고 아까 하고 동일하게 Adjacency 매트릭스와 Degree 매트릭스를 만들 수 있습니다.
고양이 사진이 첫 번째 과정인데 이렇게 이미지를 넣고 통과한 다음에 이렇게 그래프를 만드는 과정을 얘기를 하고 있습니다.
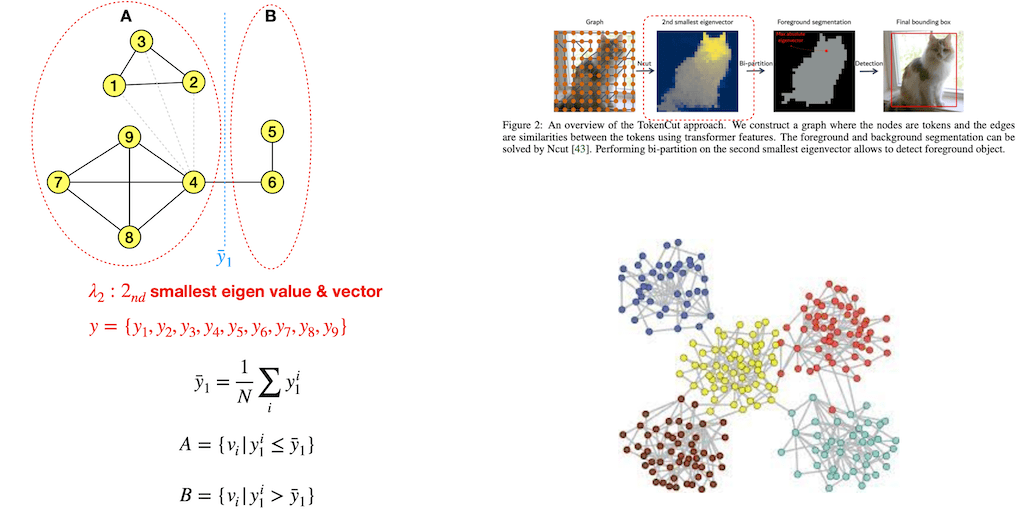
그래프를 만들었으면 이 그래프까지 만들어졌는데 4번에 연결돼 있다고 가정해보겠습니다. 이렇게 가정을 하고 봤을 때 나누는 방법을 좀 살펴보면은 여기서 2nd smallest eigen value & vector Adjacency 매트릭스와 Degree 매트릭스를 이용해서 2nd smallest eigen value & vector를 구하면 됩니다. 자세한 건 뒤에 가서 설명드리겠습니다.
다음에 보시면 eigen vector에 i값을 여기서 각 성분들을 곱하면 평균값이 이렇게 위치하게 된다고 얘기를 하고 있습니다. 그러면 y햇보다 작은 건 A, Y햇 보다 큰 건 B 이런 식으로 나눌 수 있습니다. 이것이 두 번째 그림에 있는 2nd smallest eigen value & vector를 구하는 방법과 같다고 하고 있습니다.

foreground냐 background냐 결정을 해야 되는데 아까 나눴으니까 평균값이 나오고 그러면 이 합이 같습니다. 그러면 B 쪽에 있는 값이 절댓값이 훨씬 큽니다. 그래서 이 절대값이 가장 큰 것이foreground일 것이다. 여기서는 아마 5가 갖고 있을 것 같습니다.
여기 있는 게 foreground에 있는 그 가장 max value에 있는 위치 즉, Foreground의 Seed와 같은 그런 위치라 볼 수 있습니다.
그래서 절대값 Vmax를 포함하고 있는 largest connected foreground 즉, 가장 크게 연결된 것을 foreground라고 볼 수 있다라고 얘기를 하고 있습니다.

Experiment입니다. 여기서 IoU는 CorLoc라는 걸 사용했는데 여기서는 IoU가 0.5 이상인 bounding box 개수를 TP로 보고 precision을 보이는데 보시면 아까 봤던 DINO, LOST 그다음에 지금 하고 있는TokenCut을 봤을 때 앞에 있는 것보다는 앞에 있는 DINO나 LOST에 비해서 훨씬 더 잘 잡아내고 있다 이렇게 얘기를 하고 있고 이 성능도 Token Cut이 좀 더 좋은 성능을 내고 있는 것을 볼 수 있습니다.

다음에 두 번째 Weakly Supervised Object입니다. 마지막 layer하나만 학습이 끝나고 나서 마지막 linear layer 하나만 학습했을 때 얘기를 하고 있습니다. 이때 매트릭을 세 가지로 얘기를 하고 있습니다. Top-1 Cls는 이미지 classification에서 첫 번째로 예측한 것이 맞을 확률, 그다음에 방금 봤던 GT Loc IoU 0.5인 bounding box, Top-1 Loc는 두 가지가 모두인 경우 얘기를 하고 있는데 보시면 테스트는 두 가지로 진행했습니다. ImageNet을 pretraining했고 그 다음에 ImageNet으로 Fine tune했을 때고 그 다음에 CUB라는 데이터셋으로 Fine tune했을 경우인데 Supervised의 경우는 ImageNet으로 pretraining을 하고 ImageNet에서 Fine tune을 하는 좋은 결과를 내고 있습니다.
그런데 Unsupervised의 경우에는 Token Cut이 Supervised보다 더 좋은 성능을 내고 있습니다. 이 의미는 뭐냐면 더 일반화가 잘 돼 있다 그래서 학습하지 않은 데이터를 Token Cut이 더 잘 채우고 있다고 얘기를 하고 있습니다.

그 다음에 Salient object는 가장 중요한 오브젝트를 잘 찾아냈느냐 얘기를 하고 있는데 F-measure, IoU, Accuracy 등으로 하고 있습니다. 보시면 이렇게 인풋이 있고 groundtruth가 있는데 이 친구들을 잘 잡아내고 있는 것을 보고 있습니다. 여기다가 Bilateral Solver라는 Token Cut 그러니까 Object detection을 썼더니 더 잘 된다고 얘기를 하고 있습니다.

Ablation Study입니다. τ를 0부터 이렇게 변화를 줬을 때 0.2가 가장 좋은 결과를 냈다고 얘기를 하고 있습니다. 그리고 아래쪽은 인터넷에서 받을 수 있는 이미지입니다. 이런 이미지들이 있을 때 꽤나 어려운 것임에도 불구하고 TokenCut이 잘 detection 하고 있는 것을 볼 수 있습니다.
오른쪽 그림 은은 잘 안 되는 경우를 얘기를 하고 있습니다. 그래서 보시면 LOST는 잘 됐습니다. 파란색이 정답이고, 빨간색이 예측한 건데 이런 한계들도 좀 있었다 얘기하고 있습니다.

Laplacian Matrix를 간단하게 설명드리겠습니다. 이런 그래프가 있다고 가정을 해보겠습니다. 그러면 이걸 가지고 Degree 매트릭스와 Adjacency 매트릭스를 구할 수 있습니다. 그리고 이걸 가지고 Degree 매트릭스 - Adjacency 매트릭스를 하면 이런 매트릭스를 구할 수 있습니다. 이것을 Laplacian 매트릭스라고 얘기를 하고 있습니다.
그리고 보시면 i와 j 같은 경우는 Degree 값인 거고 다음에 i와 j가 다르고 Adjacency면 - 나머지는 0인 Laplacian 매트릭스를 구할 수 있습니다.

Laplacian 매트릭스 특징은 일단 Symmetric 매트릭스입니다. 대각선 기준으로 양쪽이 같고 다음에 eigen value는 non negative real numbers이고 Eigen Vector는 real이고 Orthogonal 한 그러니까 Eigen vector들은 다 직교한다고 얘기하고 있습니다.

첫 번째가 smallest eigen vector는 모두 1이면 구할 수 있습니다. 왜냐하면 이 vector 하고 첫 번째와 곱하면 각 성분들은 다 더한 게 됩니다. 항상 다 0이 됩니다. 0이 되기 때문에 Eigen vector는 모두 x이 되고 Eigen value는 람다 값이 0이 되는 Laplacian 매트릭스에서 가장 smallest eigen value가 되겠습니다.

second smallest 구하는데 symmetric 매트릭스에서 eigen value를 구하는 것은 위 수식으로 구할 수 있다고 합니다. 그리고 아래 수식에 따라서 전개를 하면 됩니다. 기본적으로 밑에 식과 각각의 성분의 차이의 값을 최소가 되도록 하는 게 목표입니다.

보시면 여기서 가정을 두 가지를 넣어 보겠습니다. 일단은 unit vector가 맞을 수 있으니까 모든 2nd smallest eigen vector는 unit vector다. 즉 제곱의 합이 1이다라고 볼 수 있습니다. 아까 orthogonal 하다고 했기 때문에 smallest eigen vector는 모두 2였기 때문에 그래서 orthogonal 하다는 얘기는 Dot product가 0이기 때문에 Dot product가 0이 되고 결국은 모든 성분의 합이 0이 되어야만 된다는 두 가지 조건이 있습니다.

이 조건을 가지고 이렇게 볼 수 있습니다. 0을 기준으로 이 합들이 제곱합이 다 1이 달려있기 때문에 일정 범위에서 잘 분포가 되어 있어야 되고 이 사이에 이쪽에는 거리 들 만큼이 곱해질 것이기 때문에 i 제곱의 차이입니다. xi와 xj 사이기 때문에 이 선들이 최소화되도록 해야지 2nd smallest를 구할 수 있습니다. 이 선이 최소가 되는 그룹으로 나눠야 된다 이런 식으로 나눠지는 해를 구하는 게 결국은 2nd smallest eigen vector를 구하는 것과 같다고 볼 수 있습니다.




댓글