안녕하세요 콥스랩(COBS LAB)입니다.
오늘 소개해 드릴 논문은 ‘Understanding Dimensional Collapse in Contrastive Self Supervised Learning Paper explain’입니다.
해당 내용은 유튜브 ‘딥러닝 논문 읽기 모임' 중 ‘Understanding Dimensional Collapse in Contrastive Self Supervised Learning Paper explain’ 영상 스크립트를 편집한 내용으로, 영상으로도 확인하실 수 있습니다. (영상링크:https://youtu.be/dO-gD54OlO0)
제가 이번에 발표할 논문은 페이스북 AI 리서치에서 2022년 iclr에 제출한 논문인 Understanding Dimensional Collapse in Contrastive Self-Supervised Learning입니다.

먼저 Contrastive learning을 설명하려면 Self-Supervision을 알아야 합니다. Self-Supervision는 레이블이 없는 데이터셋에 대해서 다양한 pretext task를 정의를 하고 이를 풀도록 네트워크를 학습시키는 방식입니다. 이러한 pretext task로는 Context Prediction, Jigsaw Puzzle, Joint Embedding Vector 등이 있습니다. Context Prediction은 이미지 각 패치 간의 상대적인 위치를 예측하도록 하는 방법입니다. Jigsaw Puzzle은 이미지 각 패치를 섞어서 다시 원래 대로 복구시키도록 하는 방법입니다. Joint Embedding Vector은 한 이미지를 서로 다르게 Augmentation 시켜서 나오는 Embedding vector를 가지고 두 개 관계로 학습시키는 방법입니다. 설명드린 것 이외에도 많은 Self-Supervision방법들이 있습니다.

Self-Supervision만의 단점은 Collapsing Problem입니다. Collapsing Problem은 두 가지 종류가 있습니다. 첫 번째는 모든 vector가 하나의 vector로 줄어들어 버리는 complete collapse가 있고, 두 번째는 모든 선에 분포하지 않고 특정 차원만으로 학습이 되는 dimensional collapse가 있습니다. Self-Supervision는 complete collapse가 일어나진 않는데 lap score vision만이 고질적인 문제점으로서 dimensional collapse가 발생한다는 문제점이 있습니다.

다음에 Contrastive Learning입니다. Self-Supervision 중에 positive pairs는 가깝게, negative pairs은 서로 멀어지게 하는 방식이 Contrastive Learning입니다. Contrastive Learning 또한 dimensional collapse를 겪고 있습니다.

위 그림은 SimCLR로 학습시킨 모델이 Embedding space의 Singular value spectrum입니다. Embedding vectors가 총 128차원을 가질 때 Singular value들이 로그 값을 나타냈습니다. 가로축은 Singular value들의 index고, 세로축은 Singular value들의 로그 값이어서 Singular value가 0에 가까울수록 그 값이 무한하게 떨어지게 됩니다. Contrastive Learning으로 학습한 SimCLR의 경우에도 끝에 약 30개 정도 Singular value는 0에 가까운 것을 볼 수 있습니다. dimensional collapse가 많이 일어날수록 Contrastive Learning 이후에 downstream task, 예를 들어 Classification 할 때 성능이 점점 안 좋아집니다.

요약하자면 이 논문은 Contrastive Learning이 dimensional collapse를 겪고 있다는 것을 보여주고, dimensional collapse가 왜 일어나는지 두 가지 관점에서 설명을 하면서 새로운 Contrastive 방법인 DirectCLR라는 것은 제안하는 논문입니다.
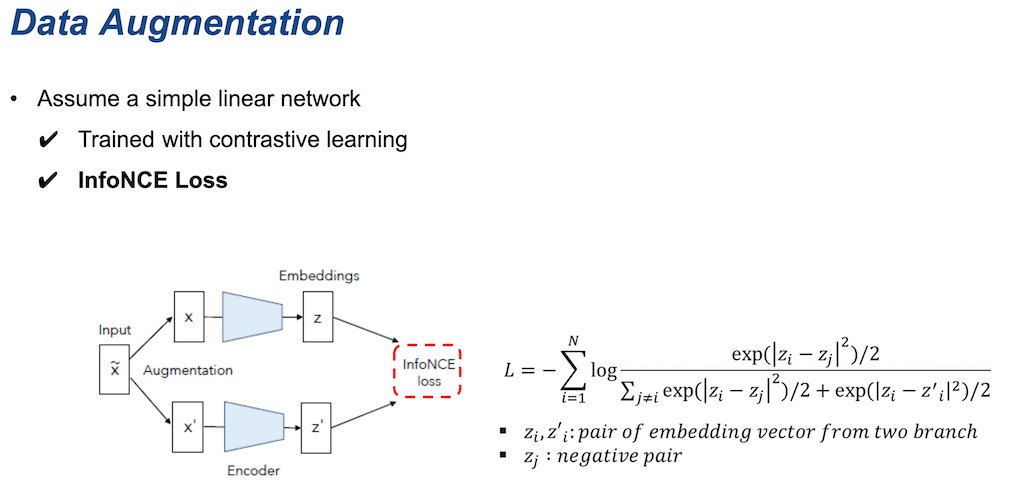
다음은 이 논문에서 주장하는 collapse가 발생하는 두 가지 메커니즘에 대해서 설명하겠습니다. 첫 번째는 Data Augmentation입니다. 논문에서 Augmentation에 의한 variance가 데이터 자체의 variance 보다 큰 경우에 dimensional collapse 발생할 수 있다고 주장합니다. 이것을 증명하기 위해서 단일 네트워크를 통해 학습을 시켰습니다. 먼저 단일 linear network 학습 시 사용한 로스는 Contrastive learning시 많이 사용하는 InfoNCE Loss입니다. 오른쪽 식은 분자에 positive pairs가 있고 분모에 negative값들이 들어가 있는 것을 알 수 있습니다.

이 식은 계산된 로스를 linear layer weight matrix W에 대해서 편미분 해 가지고 gradient chain rule을 이용해서 나타낸 식입니다. gz는 Embedding vector z를 gradient Embedding vector z를 미분한 gradient입니다. gradient G라는 게 공통적으로 모든 항에 먼저 gz가 들어가 있고, gz들은 z들로 이루어져 있고, z라는 embedding vector는 공통적으로 입력값에 weight matrix W가 곱해진 값입니다.

G는 W가 곱해져 있고 어떤 것이 곱해진 형태다라고 말할 수가 있습니다. 첫 번째 항을 보면 xi랑 xj를 뺀 것이 covariance 항입니다. i번째 데이터와 j번째 데이터 간의 covariance 항이라고 말할 수가 있고, 두 번째 항은 xi와 xi’ 간의 covariance입니다. xi'는 xi와는 데이터는 같은데 Augmentation을 다르게 한 데이터라고 보시면 되고 즉, Augmentation 한 데이터 간의 covariance라고 보시면 됩니다. 그리고 X는 두 개의 PSD 행렬의 차이입니다.

중요한 것은 X의 eigen value 부호입니다. W(t)는 weight matrix를 t번 업데이트했을 때 값을 미분방정식으로 풀고, X를 eigen decomposition 해서 대체를 한 식입니다. 학습이 진행되면서 t값이 무한대에 가까워지면 x의 eigen value에 음수 값이 있다면 X의 값은 랭크 값이 계속해서 낮아지게 됩니다. 낮은 랭크 값과 W(0)과 곱해진 W(t) 또한 low-rank가 되고 최종적으로 W 가 들어가는 covariance 역시 low-rank가 됩니다. 즉 dimensional collapse가 발생했습니다.
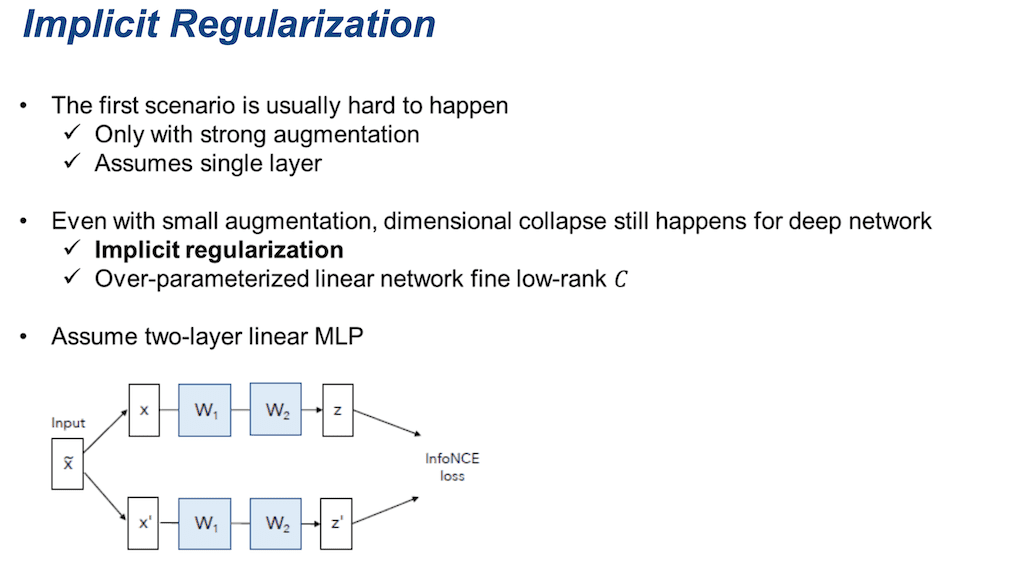
위에서 말씀드린 첫 번째 시나리오는 사실 일어나기 어렵습니다. 왜냐하면 강한 Augmentation을 가정을 해야 되고 또한 단일층의 인공신경망을 가정을 했을 때 그런 식이 전개가 되기 때문입니다. Augmentation이 적은 상황에서 deep network에서는 dimensional collapse가 안 일어나지 않습니다. 이 논문에서 dimensional collapse가 일어나는 다른 이유로 Implicit Regularization을 가정합니다. 즉 Over-parameter화 된 linear network가 low-rank Covariance를 도출한다고 설명합니다. 수학적으로 증명하기 위해서 2개 층의 MLP를 가정하였습니다.

Implicit Regularization에 대해서 설명을 해 드리도록 하겠습니다. weight matrix는 W1과 W2를 업데이트시키는 gradient 값을 표현한 식입니다. 이때 G 값은 앞에 데이터 Augmentation을 했을 때 하고 마찬가지로 아래 두 식으로 표현을 할 수 있습니다. 다만 weight matrix가 한 개가 아니라 두 개가 곱해져 있는 것을 볼 수 있고 이것을 해석하기 위해서는 두 개 사이의 상호 작용이 어떻게 되는지가 중요합니다. 두 행렬을 svd 분해를 해서 그 사이 직교 함수 v2랑 u1의 곱에 의해서 interaction이 결정을 되는 것을 알 수가 있습니다. 선형 이론 중에 만약에 x가 positive-definite 하고 모든 t에 대해서 w1, wt가 곱해진 것이 0이 아니고, 학습을 계속 무한대로 진행이 됐을 때 W1, W2의 distinctive singular values를 가진다면 행렬 A( V2tU1) 중간에 있는 interaction은 단일 행렬로 실험을 하게 됩니다.
오른쪽 그림은 실제 상황에서도 그런지 행렬 A의 절댓값을 시각화를 한 것입니다. 오른쪽 그림과 같이 단위행렬 i 하고 조금 비슷하게 나온 것을 확인할 수 있습니다.

행렬 A는 아무리 학습이 진행되어도 단일 행렬 i가 유지되도록 퇴화하지 않는 Singular value로 초기화하는 경우에 단일 행렬 i가 나옵니다. 실제 시나리오 같은 경우에는 weight matrix가 랜덤 하게 initialization 되기 때문에 alignmetn가 완벽하지 않고, 즉 단일 행렬이 나오지 않습니다. 그래서 학습이 진행됨에 따라서 퇴화하는 Singular values로 이루어진 block-diagonal 행렬처럼 나오게 됩니다. 이 경우 weight matrix의 Singular value들은 아래 두 값에 따라서 업데이트가 되게 됩니다. 아래 두 값은 weight matrix W1의 싱글 value의 k번째는 값에 따라서 업데이트가 되고 그래서 최종적으로 singular value 1k를 위와 같이 나타낼 수 있습니다.
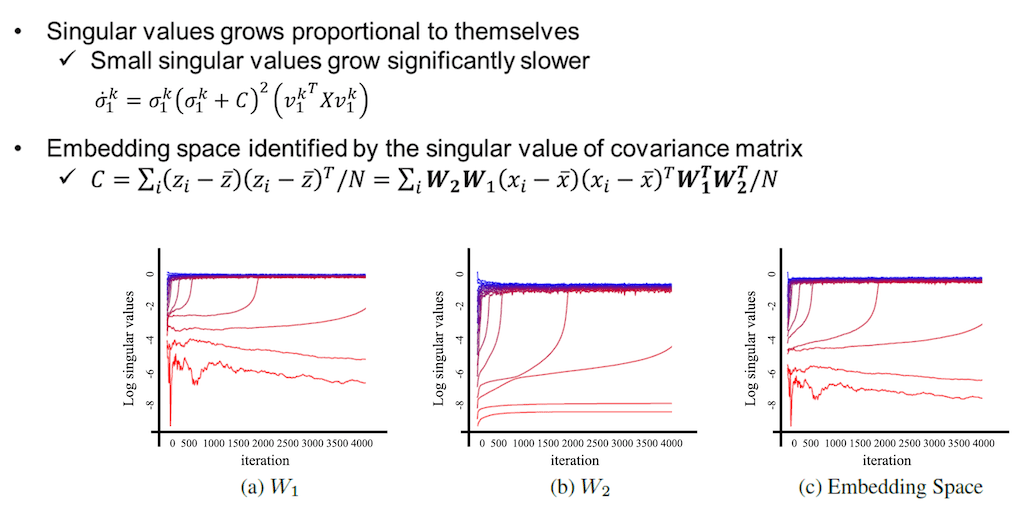
식에서 보듯이 각 Singular value들을 업데이트하는 값들이 원래 자기 자신의 값에 비례를 하는 것을 볼 수가 있습니다. 그러면 작은 Singular value들은 더욱 느리게 evolve 하고 시그마 값이 큰 Singular values들은 더 빠르게 값이 변하게 됩니다. 위 그림은 실제 실험에서 측정한 그림입니다. W1, W2에서 초기에 작은 값을 가졌던 Singular value들은 학습이 진행되면서 오히려 줄어들거나 증가하더라도 큰 값에서 시작한 Singular value 보다는 조금 느리게 커지는 모습을 보여주고, 따라서 Covariance 행렬을 Singular value에 따라서 Embedding space가 결정이 되는데 Covariance 행렬은 low-rank인 W1, W2가 곱해져 있고 따라서 Covariance matrix인 C도 low-rank가 자연스럽게 됩니다.
(c) 그림을 보시면 Embedding space 또한 학습이 진행되어도 몇몇 Singular value 들은 0에 가까운 값을 가지는 dimensional collapse가 발생을 하게 됩니다.
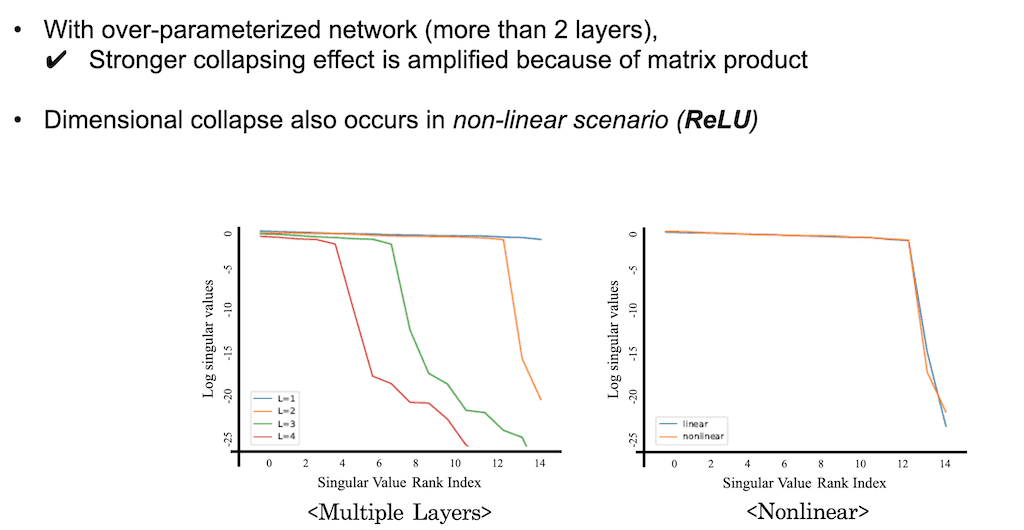
2개 층 네트워크에서 더 많은 층의 네트워크로 확장을 함으로써 오버 파라미터화 된 경우는 어떤지 실험적으로 보여줬습니다. 결과적으로는 층이 더 깊어질수록 Collapse 현상은 더욱 심해집니다. 그림을 보시면은 층 개수가 1, 2, 3, 4로 나와 있는데 L1이 1에서 4로 점점 커질수록 네트워크의 깊이가 커질수록 0에 가까운 Singular value 개수가 점점 증가하는 것을 볼 수가 있습니다. 왜냐하면 더 많은 행렬들이 곱해지면 곱해질수록 collapse가 점점 증폭되기 때문이다라고 논문에서 설명합니다. 또 추가적으로 레이어와 레이어 사이에 non-linear 한 함수를 끼워 넣었으니까 ReLU를 끼워 넣을 때도 dimensional collapse가 value가 없을 때와 비슷하게 발생을 하는 것을 확인할 수 있었습니다.
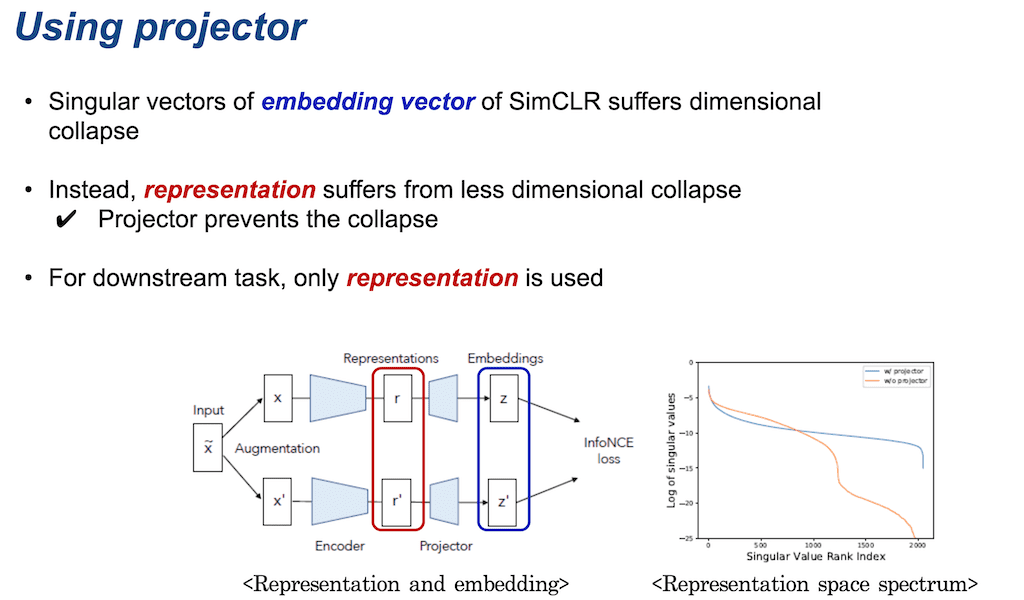
projector 없이도 projector 효과를 내는 새로운 Contrastive learning 방법인 DirectCLR를 소개를 해 드리도록 하겠습니다. SimCLR로 학습했을 때, 아래 왼쪽 그림에서 projector 이후의 Embedding vector들은 dimensional collapse를 겪습니다. 대신 projector 이전에 encoder만 통과한 representation 같은 경우에는 오른쪽 그림과 같이 dimensional collapse가 덜 심한 것을 볼 수 있습니다. 만약에 projector가 없이 바로 직접적으로 representation만 가지고 InfoNCE 로스를 구성을 해서 학습을 시키면 dimensional collapse을 겪게 되는 것을 나타낸 것이 오른쪽 표입니다. 노란색선은 projector 없이 학습한 representation들의 Singular value spectrum이고 파란색은 projector를 사용함으로써 학습된 representation들의 Singular value spectrum입니다.
그리고 SimCLR 같은 경우에는 projector들은 downstream task를 수행할 때는 projector가 버려지고 representation만 사용이 됩니다.

projector라는 게 어떤 형태를 가지고 그리고 어떤 영향을 미치는지 설명드리겠습니다. 먼저 projector의 weight matrix는 diagonal 한 형태일 것이라고 추측을 할 수가 있습니다. projector인 weight matrix가 encoder의 weight matrix와 정렬이 발생을 하면서 projector의 두 직교 함수가 합쳐지면서 단일 행렬화 되고 이는 즉, 단순히 projector는 대각 행렬의 형태만 학습이 진행됩니다. 그래서 이런 projector는 low-rank이기 때문에 projector 이전의 representation 또한 low-rank의 representation만 전달을 하게 됩니다.
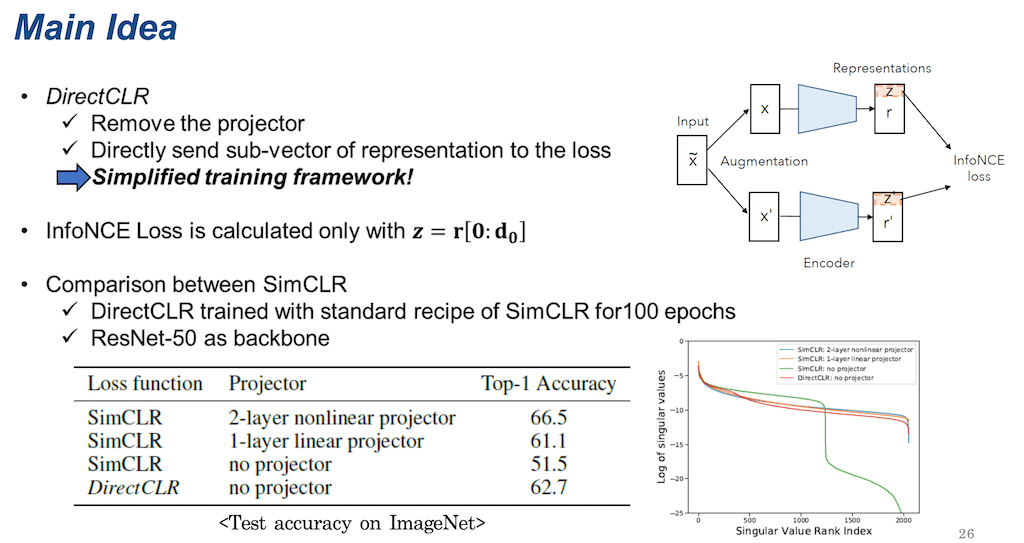
projector가 low-rank의 representation에만 영향을 미치는 거면은 projector를 없애고 디렉트 하게 representation만을 사용을 하되 low-rank의 서브 vector만 가지고 로스를 계산하면 비슷한 효과를 낼 수 있지 않을까, 그러면 이 SimCLR의 학습방법이 좀 더 간소화될 수 있지 않을까라고 생각을 해서 나온 게 DirectCLR입니다.
DirectCLR는 representation vector에서는 오직 서브 vector만으로 로스가 계산돼서 학습이 됩니다. DirectCLR 성능을 SimCLR 하고 비교를 하기 위해서 SimCLR의 표준 학습 방식으로 100 epoch 동안 ResNet 50에서 학습을 시켰고, 이후 ImageNet에 대한 성능을 비교하면 위 표와 같이 나옵니다.
보시면 2개의 레이어의 projector를 사용했을 때만큼의 SimCLR보다는 아니지만 1개 층을 사용했을 때보다 61.1 보다는 조금 더 높은 62.7 정도의 정확도를 보여줍니다. 각각 4개의 경우에 대해서 Singular value의 spectrum을 시각화한 것이 오른쪽 그래프입니다. DirectCLR은 빨간색 선입니다. DirectCLR가 projector가 없이 학습했음에도 불구하고 projector를 써서 dimensional collapse를 예방했다고 보이는 SimCLR만큼 Singular value 값들이 존재하고, SimCLR인데 projector가 없으면 되게 빠르게 0에 가까운 값들이 많은 것을 볼 수 있습니다.
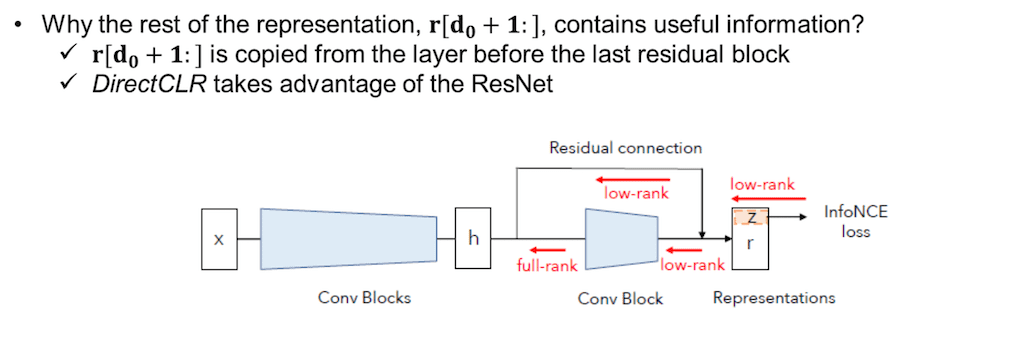
의문이 들 수 있는 게 gradient는 오직 representation의 일부만 사용을 했는데 왜 정확도 측정은 ResNet의 결괏값으로 나온 representation 전체를 이용해서 학습을 시켰는가 하는 것입니다. 그러면 나머지 부분에도 유용한 정보가 학습이 되기는 한 건가라고 의문이 들 수가 있습니다. 결론적으로 말씀드리면 유용한 정보가 들어 있긴 합니다. 왜냐면은 r [d0+1:]는 사실 Resnet의 마지막 Convolution의 앞에 있는 Residual connection을 통해서 카피된 값들이기 때문입니다. 카피된 값들도 InfoNCE 로스를 미분해서 gradient가 직접적으로 전달되지는 않지만 어쨌든 Conv Block이 학습되면서 업데이트되기 때문에 유용한 정보를 담고 있는 것이다라고 설명합니다.

마지막으로 Conclusion입니다. 먼저 이 논문 DirectCLR는 dimensional collapse에 대한 이론적인 근거를 Strong Augmentation과 Implicit Regularization 두 가지 관점으로 설명을 했습니다. 그렇게 해서 새로운 Contrastive self Supervised learning인 DirectCLR를 제시했습니다. DirectCLR는 projector가 없음에도 불구하고 dimensional collapse를 예방할 수가 있었고, SimCLR가 한 개 리니어의 projector를 썼을 때보다 조금 더 좋은 성능을 낼 수가 있었습니다. 다만 한계점으로는 DirectCLR는 두 개의 레이어의 projector를 사용했을 때보다는 성능이 별로 좋지가 않고, Residual connection 통해서 유용한 정보를 그대로 불러올 수 있는 다른 종류의 네트워크로 들어오는 일반화가 어렵지 않을까 하는 그런 한계점이 존재했습니다.




댓글