안녕하세요 딥러닝 논문 읽기 모임입니다.
오늘 소개해 드릴 논문은 'A Normalized Gaussian Wasserstein Distance for Tiny Object Detection'입니다.
해당 내용은 유튜브 ‘딥러닝 논문 읽기 모임' 중 ‘A Normalized Gaussian Wasserstein Distance for Tiny Object Detection’ 영상 스크립트를 편집한 내용으로, 영상으로도 확인하실 수 있습니다. (영상링크:https://youtu.be/eGKlg4sZ0Zw )

COCO Dataset에서 정의한 Object 크기는 Large, Medium, Small로 구분이 되어 있습니다. Large는 96 X 96픽셀 이상, Medium은 32 X 32부터 96 X 96픽셀 사이, Small은 32 X 32픽셀 이하를 의미합니다.
작은 것들을 내포하는 데이터셋은 대표적으로 AI TOD(Tiny Object Detection) 데이터셋이 있습니다. Tiny Object Detection에서는 Tiny랑 very Tiny까지 포함되어 있습니다. Tiny는 8 X 8부터 16 X 16이고, Very Tiny는 그 이하를 의미합니다.

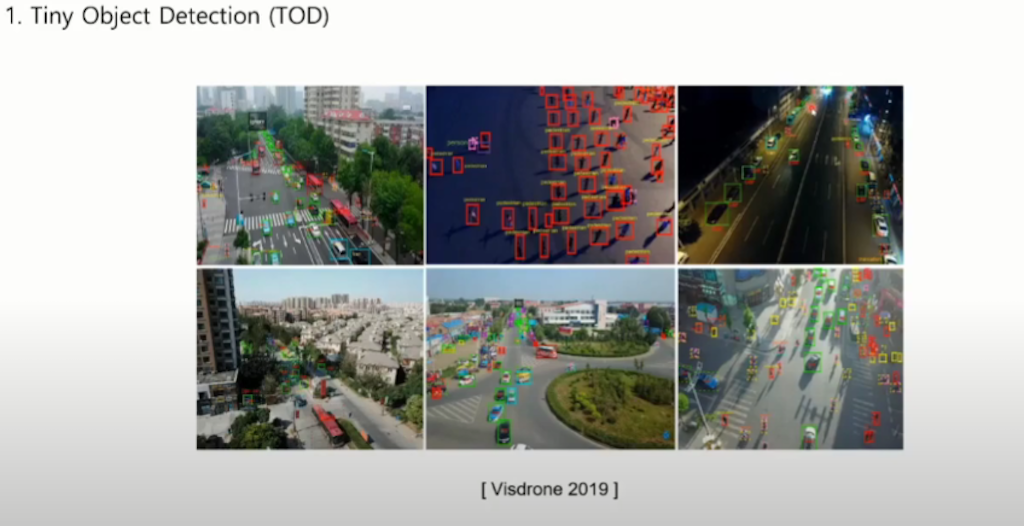
논문에서 실험을 진행한 데이터셋은 위성과 드론에서 촬영한 영상입니다. Object들이 매우 작고 다양하게 포함이 되어 있는 것을 확인할 수 있습니다.
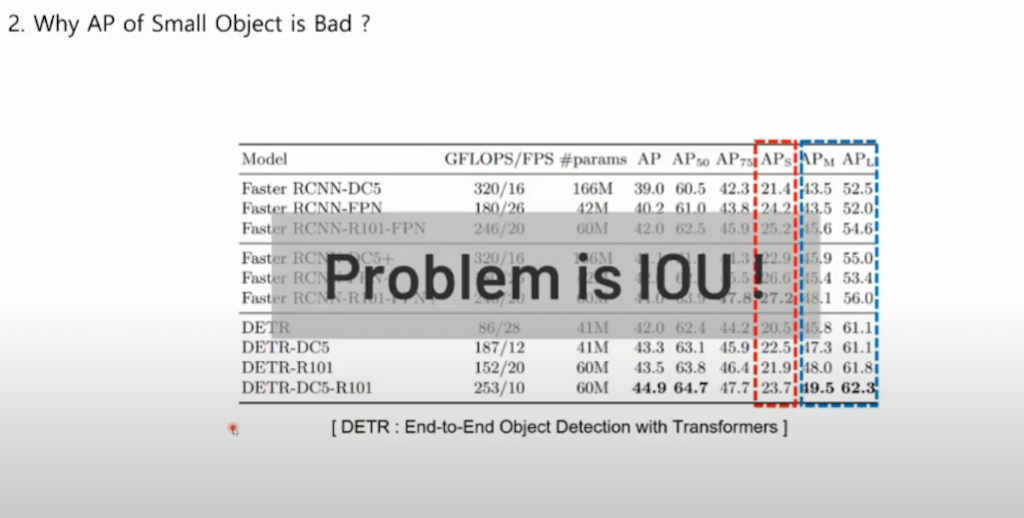
APS는 APM이나 APL보다 낮은 성능을 보이는 것을 확인할 수 있습니다. 논문에선 작은 객체들에 대해서 탐지 능력이 떨어진 원인을 IoU가 문제라고 설명하고 있습니다.

왜 IoU가 Small Object를 탐지하는데 문제가 되는지 설명드리겠습니다. 왼쪽이 작은 크기의 박스고 오른쪽이 큰 크기의 박스입니다. 박스 B와 C는 각각 A 박스를 기준으로 1 Pixel, C는 4 Pixel이 translation 되어 있습니다. 왼쪽 A와 B 의 IoU를 보시면은 0.53이고 오른쪽 A와B는 0.9 입니다. 같은 크기만큼 translation이 되었음에도 불구하고 IoU값이 차이가 나는 것을 확인할 수 있습니다. 4 Pixel이 움직인 A 와 C는 IoU가 0.65이고 크기가 작은 박스에 경우 0.6인 것을 확인할 수 있습니다. translation시 박스 크기에 따라서 metric이 변한다라는 게 IoU의 문제라고 설명하고 있습니다.
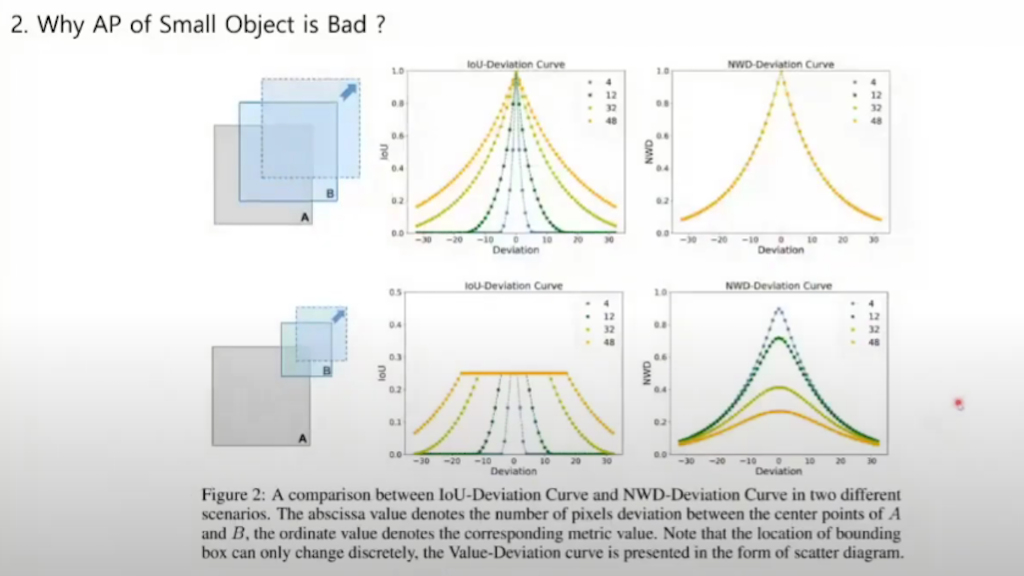
위 그림은 동일한 크기의 A와 B의 박스를 비교한 것이고 아래는 다른 크기의 박스를 비교한 것입니다. 색상은 박스 크기를 나타내고요. IoU의 metric은 박스 크기가 같은 경우에 박스 크기에 따라서 IoU가 급격하게 증가하거나 감소하고 박스가 커지면 커질수록 그래프의 기울기와 완만해지는 것을 확인할 수 있습니다.
오른쪽은 논문에서 제안하는 방법인 NWD입니다. NWD는 박스의 크기와 상관없이 동일한 기울기를 가진 metric을 확인할 수 있다고 설명을 하고 있습니다.
크기가 다른 경우에도 IoU를 사용할 경우에는 크기가 다르기 때문에 일정 IoU이상은 존재하지 않습니다. 최대 IoU는 B크기만큼만 되기 때문에 B크기 이상으로는 IoU가 존재할 수가 없지만 NWD를 쓰면 다르게 IoU를 나타낼 수 있습니다.

학습 과정입니다. detection 모델에서 나온 결과 박스들을 가지고 Loss를 계산하고, backpropagation을 진행합니다. 이때 Loss를 계산하기 위해서는 ground truth Box랑 차이를 계산합니다.

Label Assignment은 수많은 박스들 중 ground truth를 선정하는 방법입니다. 보통은 ground truth와 가장 IoU가 높은 예측 박스 중에 선정을 해서 ground truth를 계산합니다. 이때 IoU가 작은 물체는 Negative Sample, 즉 background라고 생각합니다. 혹은 ground truth가 가장 높은 것은 Object라고 생각하고 Loss를 계산합니다. 일반적으로는 IoU Threshold를 미리 정해 놔서 일정 IoU이하는 전부 Negative Sample로 결정하는 박스 Assignment를 합니다.

IoU가 어떤 영향을 끼치는지 살펴보겠습니다. 그림에서 A 가 GT(Ground Truth)고 B와 C가 예측된 박스라고 생각했을 때 IoU는 0.9입니다. 일정 Threshold이하면 모두 Negative Sample으로 할당돼서 악영향을 끼칠 수도 있습니다. Tiny Object에서 IoU를 사용하면 빈번하게 발생할 수 있는 문제라고 설명하고 있습니다.

다음은 NMS(Non-Maximum Suppression)입니다. IoU가 사용되는 부분은 NMS에서도 사용됩니다. NMS는 inference에만 사용되긴 하지만 NMS에서도 IoU가 사용되기 때문에 문제가 될 수 있다고 설명하고 있습니다. 또한 IoU Loss를 사용하는 Regression Layer에서도 학습과정에서 악영향을 끼칠 수 있다라고 설명을 하고 있습니다.

작은 물체를 잘 못 찾는 문제를 해결하기 위해 매우 보편적으로 쓰고 있는 방법인 FPN(Feature Pyramid Network)입니다. Feature 크기를 다양하게 변화시켜서 다양한 크기의 물체를 잘 잡게 만들고 있습니다.

ATSS는 Label Assignment 문제를 해결하기 위해서 만든 방법입니다. handcraft component인 IoU Threshold를 자동으로 결정을 해 주는 방법입니다.

IoU 문제를 해결하기 위한 방법입니다. GIoU, DIoU, CIoU 은 IoU를 대체하기 위해서 나왔습니다. 두 박스가 겹치지 않을 경우에는 IoU가 0으로 떨어지기 때문에 얼마나 박스가 떨어져 있는지 확인을 못 하기 때문에 두 박스 사이의 거리나 면적들을 가지고 IoU를 보완하겠다 라는 개념입니다.

NWD에서 Wasserstein Distance는 두 확률분포 사이에 Distance를 계산하는 방법입니다. infinum은 최솟값을 찾는 과정이고, X-Y는 Distance expectation, 즉 X와 Y 분포의 distance의 기댓값 중에서 가장 작은 값을 취합니다.

Method입니다. NWD는 두 개 probability Distribution을 가지고 distance를 계산합니다. 이를 위해서 Bounding Box를 2D Gaussian Distribution으로 Modeling 합니다. 2D Gaussian Distribution 수식을 Density Contour로 나타내면 Mahalanobis distance를 상수 K로 나타냅니다. K값에 따라서 Gaussian Distribution의 오차율이 다르게 나옵니다.

Bounding Box Component를 가지고 타원 방정식을 구해서 Density Contour까지 구해보겠습니다. Bounding Box가 있을 때 내접하는 타원의 Component는 중심점 그리고 width랑 height가 있습니다. 위에서 설명드린 Mahalanobis distance가 1일 때 타원 방정식과 Density Contour 방정식은 서로 매칭이 될 수 있습니다. U는 일반적으로 Gaussian Distribution에서 말하는 평균값이고 ∑는 공분산 행렬입니다.

Gaussian Wasserstein Distance에 적용해봤습니다. 이 Gaussian Wasserstein Distance는 Gaussian Distribution 사이에 계산된 Wasserstein Distance의 공식입니다. 공분산 행렬이므로 교환 법칙이 성립합니다.

교환법칙이 성립한다고 계산하면 m은 U이므로, U값과 공분산 행렬을 수식에 대입해서 전개를 하였습니다. 각 Bounding Box 요소들 간의 Euclidean distance처럼 간단하게 나타낼 수 있습니다.
IoU metric은 0부터 1까지 Normalize 됐지만 Wasserstein Distance 같은 경우에는 Normalize 돼있지 않기 때문에 metric으로 활용하기 위해서 exp함수를 사용을 해 0부터 1까지로 Normalization 하게 되고 여기서 나타낸 C 같은 경우는 하이퍼 파라미터입니다.

Label Assignment와 NMS 그리고 Regression Loss의 IoU Loss 대신에 사용할 수 있게 적용을 해서 실험했습니다.

Experiments 부분입니다. 실험에서 사용한 Baseline 네트워크는 Fast R CNN을 사용했습니다. 다른 metric과 비교해 봤을 때 Tiny Object Detection에서 제일 효과가 좋은 것을 확인할 수 있습니다. 다른 metric들을 적용해봐도 효과가 별로 안 좋은데 NWD를 적용했을 때 효과가 좋은걸 확인할 수 있습니다.

각 모듈에도 적용해가면서 평가해봤습니다. Label Assigning에서 제일 효과가 좋은 것을 확인할 수 있고 NMS에 적용했을 때는 오히려 성능이 떨어지거나 조금 오르고, Loss에 사용했을때는 성능 상승폭이 적었습니다.

여러 모듈에서도 테스트를 해 봤을 때 역시 NWD를 사용하는 게 효과가 제일 좋은것을 확인할 수 있습니다.

실제 실험 결과입니다. 위쪽은 IoU를 사용했을 때 밑에는 NWD를 사용했을 때입니다. 초록색은 잘 찾은 부분이고, 빨간색은 찾아야 되는데 못 찾은 부분, 파란색은 못 찾아야 되는데 찾은 부분입니다. NWD를 사용하는 게 효과적인 것을 확인할 수 있습니다.

전체 비교 테이블입니다. 별표가 있는 것이 NWD를 적용한 네트워크입니다. 그래서 DetectoRS를 적용했을 때 제일 효과가 좋은 것을 확인할 수 있습니다. 그리고 또한 Tiny랑 Very Tiny에서는 효과가 좋은 걸 확인할 수 있는데 s나 m에서는 효과도 안 좋은 것도 있습니다.

결론을 내자면 IoU를 대체하는, NWD 사용하는 게 되게 간단한 방법이고 코드 구현도 간단하면서 효과적으로 Tiny Object Detection을 수행할 수 있습니다. 그러나 실제 구현해보니 큰 Object에는 오히려 성능이 떨어지는 것을 확인할 수 있었습니다.
'이미지 처리 논문' 카테고리의 다른 글
| 진보된 detection technique- YOLOX (0) | 2022.05.18 |
|---|---|
| MobileViT: Light-weight, general-purpose, and Mobile-friendly Vision Transformer (2) | 2022.05.16 |
| Dense vs Sparse - Sparse R-CNN (0) | 2022.05.16 |
| Pose Estimation논문! Transfer Learning for Pose Estimation of Illustrated Characters (0) | 2022.05.16 |
| Transfer Learning에 관해서… How transferable are features in deep neural networks? (0) | 2022.05.16 |




댓글